我们首先讨论非负权网络的最短路求法。在这类网络中的最短路具备这样一个基本的性质，这一性质是求解最短路问题的基本依据，即如果P是D中从vs到vt的最短路，那么P中某一点vi到vt的最短路也是沿着P的。

目前公认最好的方法是由Dijkstra于1959年提出的。该方法的主要特点是以起始点vs为中心向外层层扩展，直到扩展到终点vt为止。求解过程中，与每个点对应，记录下一个数（称为这个点的标号），它或者表示从vs到该点的最短路的权（称为P标号或永久标号），或者是从vs到这点的最短路的权的上界（称为T标号或临时标号）。事实上是将网络中的点划分为P和T两个集合。方法的每一步是去修改T标号，并且把某一个具有T标号的点改变为具有P标号的点，从而使D中具有P标号的顶点数多一个，这样至多经过p-1步就可以求出从vs到各点的最短路。

在具体的求解过程中，关键问题有两个：一是如何修改T标号；二是依据什么标准将T标号点变为P标号点。以图6-14为例，因为所有的wij≥0，d(v1,v1)=0为最短距离，所以v1是具有P标号的点，其余点均属于T标号的点。考察从v1出发的两个弧(v1,v2)和(v1,v3)。如果从v1出发沿(v1,v2)到达v2，路线的距离为d(v1,v1)+w12=9，而沿(v1,v3)到达v3的距离为d(v1,v1)+w13=8。因为min{9,8}=8，所以从v1出发到v3的最短距离必定是8，这是因为所有的权均非负，从v1经其他点（v2）再到v3的距离必然不会小于8。于是将v3纳入P标号点的集合，其标号为8。接下来考虑从v1和v3出发所到达的最近的点，目前从v1出发沿(v1,v2)到达v2，路线的距离为d(v1,v1)+w12=9，v3沿(v3,v4)到v4的距离为d(v1,v3)+w34=16，v3沿(v3,v6)到v6的距离为d(v1,v3)+w36=15。这三个距离中，最小的为v1到v2的距离，基于前述相同的理由，将v2变为P标号点，其标号为9。一直重复这一过程，直到v7得到P标号为止，即可得从v1出发到各点的最短路线与距离。

现将Dijkstra标号法求网络的最短路的过程总结如下：

(1)给vs以P标号0，其他点给T标号M。

(2)从刚得到P标号的点（vk）出发，按下式修改与其相邻的所有具有T标号的点的标号:min{T(vj),P(vk)+wkj}。

(3)从所有具有T标号点中选取一个最小值，将其改为P标号，然后重复步骤(2)，直至所有点都得到P标号。

例6.4(Dijkstra标号法)利用Dijkstra标号法求解图6-14所示网络中从v1到v7的最短距离。

解第1步给v1标P标号0，其余点标T标号M（圈中数字为永久标号），如图6-15所示。

第2步从v1出发修改与其相邻的具有T标号的点v2和v3。如图6-16所示，v2的标号为

v3的标号为

第3步在所有T标号的点中将具有最小标号的点（v3）变为永久标号，如图6-17所示。

图6-15　第1步

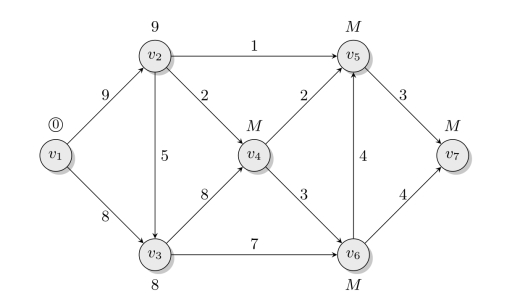
图6-16　第2步

图6-17　第3步

第4步从刚得到P标号的点v3出发修改与其相邻的具有T标号的点v4和v6。如图6-18所示，v4的标号为

v6的标号为

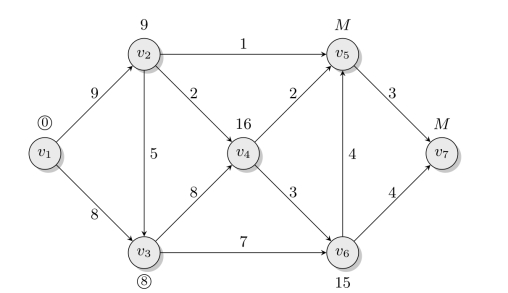
图6-18　第4步

第5步在所有T标号点中选取最小的标号点（v2），将其变为P标号点，如图6-19所示。

图6-19　第5步

第6步从新得到P标号的点v2出发修改与其相邻的T标号点v4和v5。如图6-20所示，v4的标号为(www.daowen.com)

v5的标号为

图6-20　第6步

第7步在所有T标号点中，将标号最小的点v5变为P标号点，如图6-21所示。

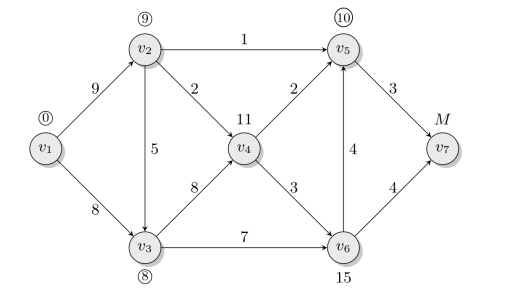
图6-21　第7步

第8步从新得到P标号的点v5出发修改与其相邻的T标号点v7。如图6-22所示，v7的标号为

第9步在所有T标号点中，将具有最小标号的点v4变为P标号点，如图6-23所示。

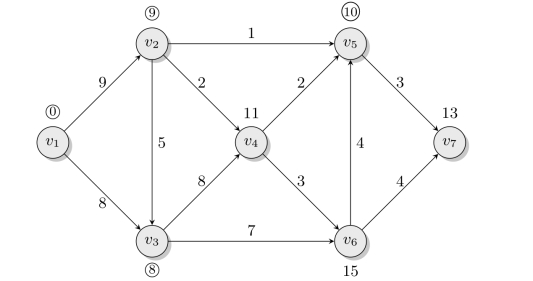
图6-22　第8步

图6-23　第9步

第10步从新得到P标号的点v4出发修改与其相邻的T标号点v6。如图6-24所示，v6的标号为

第11步在所有T标号点中将标号最小的点v7变为P标号点，如图6-25所示。

第12步从新得到P标号的点v7出发修改与其相邻的T标号点。没有这样的点，跳至下一步。

第13步在所有T标号点中将最小标号点v6变为P标号点，如图6-26所示。

图6-24　第10步

图6-25　第11步

图6-26　第13步

至此所有的点均得到了P标号，表明找到了从v1出发到各点的最短路线与距离。最短距离即为各点标号，最短路线如图6-27所示。

图6-27　最短路问题