现实中经常遇到一类问题：寻找在一个网络中从某点到另一点的最短距离。典型的，如图6-14所示的交通网络中，每条弧旁边的数字表示两点之间的距离。若从v1出发，到达v7的最短路线是什么呢？

从图中可以发现，从v1出发到达v7有许多线路可供选择，而且每一条线路的距离也是不同的。如路线v1→v2→v5→v7的距离为13，而路线v1→v3→v4→v5→v7的距离为21。如果依靠列举方法得到所有可能的路线与距离，显然是不可行的。我们将最短路问题描述为：在一个给定的有向图D=(V,A)中，对于每一条弧相应地有权w(vi,vj)=wij；又给定D中的两个顶点vs和vt，设P是D中从vs到vt的一条路，定义路P的权是P中所有弧的权之和，记为w(P)；最短路问题就是要在所有从vs到vt的路中，求一条权最小的路，即求一条从vs到vt的路P∗，使

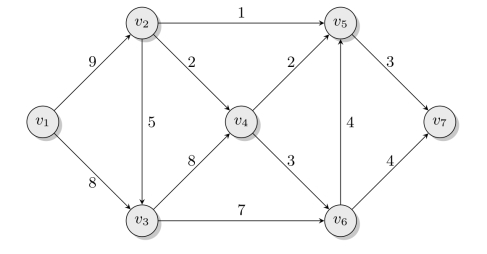
图6-14　最短路问题(www.daowen.com)

式中对D中所有从vs到vt的路P取权最小，称P∗是从vs到vt的最短路。路P∗的权称为从vs到vt的距离。

最短路问题是重要的最优化问题之一，它不仅可以直接应用于解决生产实际的许多问题，如管道铺设、线路安排、厂区布局、设备更新等，而且经常被作为一个基本工具，用于解决其他的优化问题，如后面会遇到的最小费用最大流问题。