背包问题是动态规划中的一个经典问题。有一个人带一个背包上山，其可携带物品重量的限度为a千克，设有n种物品可供他选择装入背包中，其中第i种物品每件的重量为wi千克，在上山过程中的作用（或价值）是携带数量xi的函数ci(xi)，问此人应如何选择携带物品（各几件），以使得所起作用（总价值）最大？这是一维背包问题，如果还考虑背包容量并已知不同物品的体积，那么这就成为二维背包问题。背包问题在现实中有着广泛的应用，类似的问题有工厂里的下料问题、运输中的货物装载问题、卫星内的物品装载问题等。下面用一个实例来说明利用动态规划求解背包问题的基本思路。

例5.9(背包问题)某货运汽车的载重量为13吨，现需运送5种货物。货物的重量及其运送单件货物的利润如表5.9所示。试确定如何装载这些货物，使运输利润最大。

表5.9　货物重量及其单件运输利润

解首先根据货物单位重量的价值（即用单件货物利润除以单件货物重量）将货物排序，结果如表5.10所示。

表5.10　货物重量及其单件运输利润

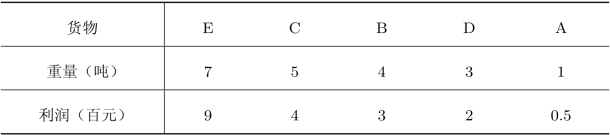
然后根据表5.10按货物的种类将问题划分为5个阶段，即k=1,2,···,5。设xk为第k种货物的装载数量，且要求xk为整数；sk为第k种货物至第5种货物可用的装载重量，则s1=13。设第k种货物的单件重量为wk，单件货物利润为rk，则装载第k种货物xk件时的利润为rkxk。状态转移方程为

fk(sk)为最优值，表示从第k种货物至第5种货物按最优装载量计算得到的最大利润值。则该问题的基本方程为

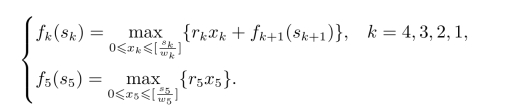
其中，[·]为取整运算。

当k=5时，

当k=4时，有

当k=3时，有(www.daowen.com)

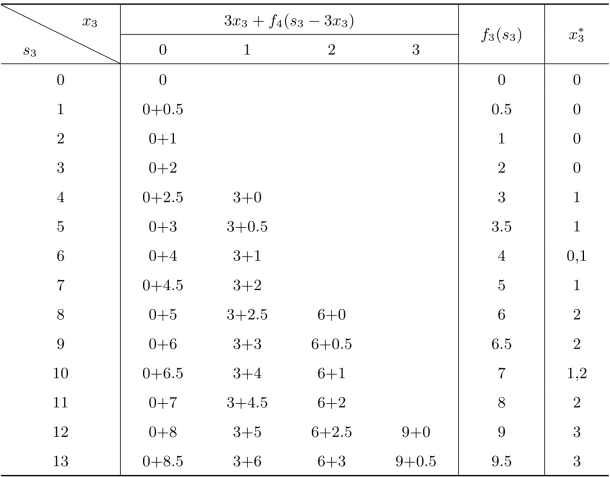
具体计算过程如表5.11所示。

当k=2时，有

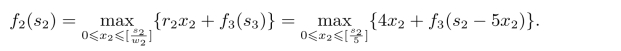
由于排在第一位的货物E的单件重量为7，所以s2取值为13或者6，因此x2可取1或者2。

若x2=1，则s2=6，f2(s2)=4.5。

若x2=2，则s2=13，f2(s2)=10。

表5.11　背包问题计算表

当k=1时，由于s1=13，所以x1可取0或者1，所以

若x1=1，则f1(s1)=9+4.5=13.5。

若x1=0，则f1(s1)=0+10=10。

所以第一阶段的最优决策为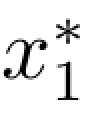=1。根据上述求解过程逆推得到该问题的最优决策为

即货物E,C,A各运1件，最大利润为13.5百元。

由上述求解过程发现，背包问题求解过程中由于要求决策变量必须是整数解，所以增加了求解过程的复杂性。一般情况下，应先将货物按单位重量价值进行降序排列，而且在求解过程中还要结合问题的具体参数作出适当的调整，在较简单情况下可以利用分析得到某步的决策，如果情况复杂可充分利用表格的方式进行求解。