生产计划问题是：设某企业对某种产品要制订一项n个阶段的生产计划，已知它的初始库存量为零（为简单起见），每阶段生产该产品的数量有上限的限制；每阶段市场对该产品的需求量是已知的，企业要保证满足需求；在n阶段末的终结库存量为零（为简单起见）。问该公司如何制订每个阶段的生产计划，从而使总成本最小?

生产计划问题如果用于商业经营企业也是可以的，这时需要决策的是进货计划。

设dk为第k阶段对产品的需求量，xk为第k阶段该产品的生产量（或采购量），sk为第k阶段结束时的产品库存量，则有

设ck(xk)表示第k阶段生产产品量为xk时的成本，一般而言它包括生产的固定成本K和可变成本axk（其中a为单位可变成本），即

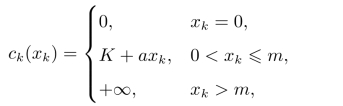
其中m为企业的单阶段的最大生产能力。

设hk(sk)为第k阶段结束时有库存量sk所需的存储费用。所以，第k阶段的总费用为ck(xk)+hk(sk)。令最优值函数fk(sk)表示从第1阶段初到第k阶段末库存量为sk时的最小总费用，则可以得到该问题的顺序递推方程为

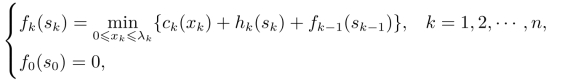
其中λk=min{sk+dk,m}。

例5.8(生产计划问题)某工厂在未来6个月中面临着如表5.8所示的供货需求，要求每月底交货。已知该厂的生产能力为每月4百件，该厂仓库的存货能力为3百件，每百件货物的费用为1万元，而且在进行生产的月份，工厂要支出日常费用0.4万元。仓库存储费用为每百件每月0.1万元。假设开始时及6月底交货后无存货。试问应在每个月各生产多少件产品，才能既满足供应需求又能使总费用最小？

表5.8　工厂未来6个月的供货需求（单位：百件）

(www.daowen.com)

解设用前述符号，按6个月份将此问题划分为6个阶段。根据题设条件，该工厂的第k月的生产成本为

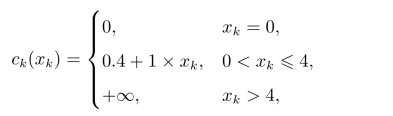
第k月的存储费用为hk(sk)=0.1sk。

(1)当k=1时，有

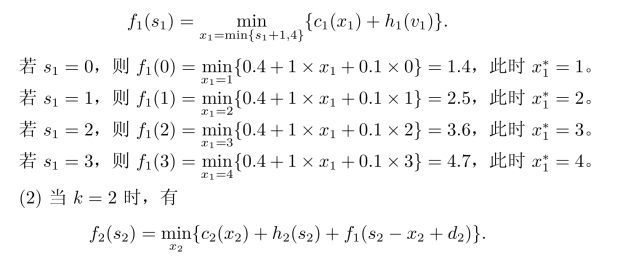
此时，考虑到后续要求与最大生产能力，s2至少应为1，而x2的取值一方面要保证当前需求d2还要保证既定的s2，所以它的范围是变化的。

若s2=1，则

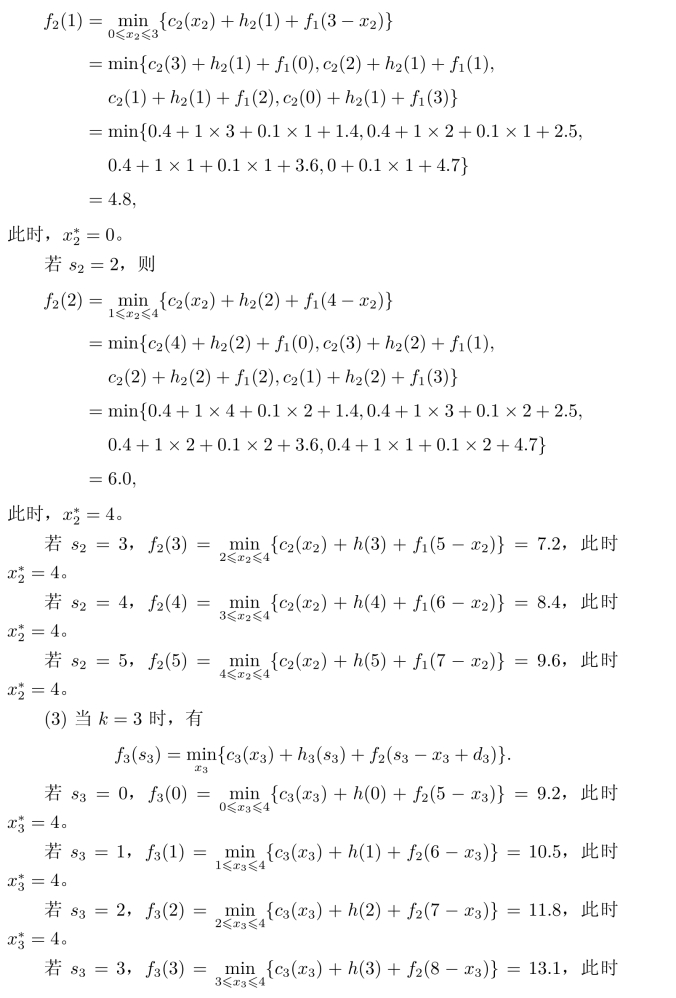
最后按计算顺序反推算，可得到每个月份的最优生产决策为

最小费用为16.1万元。