资源分配问题是将数量一定的一种或若干种资源适当地分配给多个使用者,从而使得所有使用者总的效益最好。根据资源的种类数量,可以分为一维资源分配问题和多维资源分配问题。根据资源的数量是否连续,可分为离散资源分配问题和连续资源分配问题。这里重点介绍一维资源分配问题。
1.离散的一维资源分配问题
离散的一维资源分配问题描述如下:现有某种资源,其数量为q,用于生产n种产品,若分配数量xi用于生产第i种产品,其收益为ri(xi),问应如何分配这种资源,才能使生产n种产品的总收益最大?
这个问题的静态规划模型为
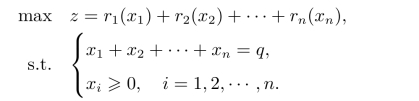
在该模型中,如果ri(xi)为线性函数,则它是一个线性规划问题;如ri(xi)为非线性函数,则它是一个非线性规划问题。但当n较大时,求解较为繁琐。所以,对于这一类问题可以考虑使用动态规划方法进行求解。
根据动态规划的求解思路,可以将上述静态规划问题转化为如图5-5所示的动态规划问题。
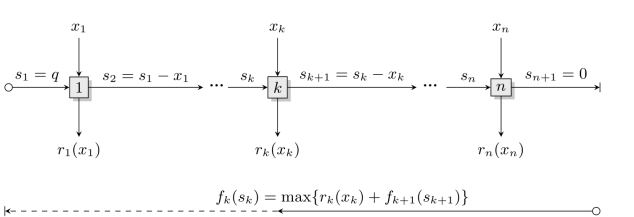
图5-5 离散的一维资源分配问题
动态规划模型建立过程如下:
设状态变量sk表示分配用于生产第k种产品至第n种产品的资源数量,则s1=q;设决策变量xk表示分配给生产第k产品的资源数量,则状态转移方程为
![]()
允许决策集为Dk(sk)={xk|0≤xk≤sk}。
令最优值函数fk(sk)表示以数量为sk的资源分配给第k种产品至第n种产品所得到的最大总收入。动态规划的逆推方程为
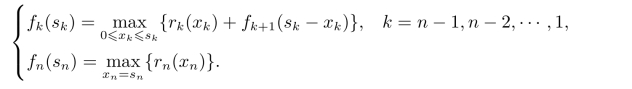
例5.6(离散的一维资源分配问题)某公司打算在三个不同的地区设置4个销售点,根据市场预测部门估计,在不同的地区设置不同数量的销售店,每月可得到的利润如表5.4所示。试确定各个地区设置多少个销售点,才能使每月获得的总利润最大。
表5.4 不同地区设置不同数量销售店的收益

解将问题按地区划分为三个阶段,k=1,2,3分别表示地区1,2,3。设sk为分配给第k个地区到第3个地区的销售店数,xk为分配给第k个地区的销售店数,则0≤xk≤sk且有sk+1=sk-xk。rk(xk)为分配xk个销售店给第k地区的收益值,fk(sk)为sk个销售店分配给第k个地区到第3个地区时所得到的最大收益值。这样得到动态规划的基本方程为

当k=3时,
![]()
s3可能取值为0,1,2,3,4,由于此时只有一个区域,所以 =s3。其数值计算如表5.5所示。
=s3。其数值计算如表5.5所示。
当k=2时,s2可能取值0,1,2,3,4,根据基本方程
![]()
计算过程如表5.6所示。
表5.5 离散一维资源分配计算表(一)
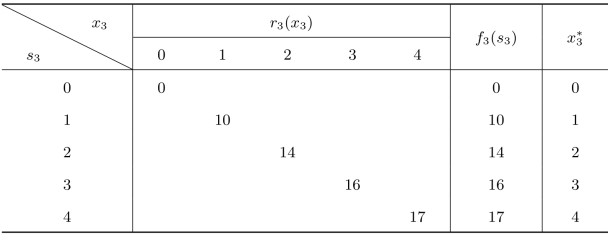
表5.6 离散一维资源分配计算表(二)
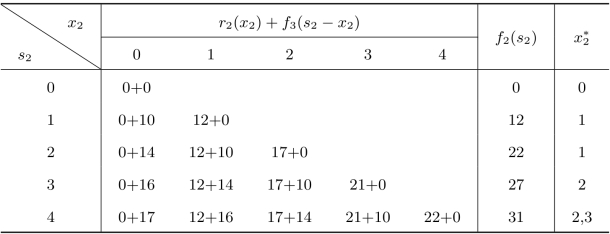
当k=1时,s1=4,根据基本方程
![]()
计算过程如表5.7所示。
表5.7 离散一维资源分配计算表(三)(https://www.daowen.com)

最后根据计算表格的顺序反推算,可以得到该问题的最优分配方案为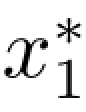 =2,
=2,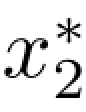 =1,
=1, =1,最大收益为47。
=1,最大收益为47。
上述即为离散的一维资源分配问题,在现实中如原材料分配、投资分配、货物分配等问题,都属于这类问题。
2.连续的一维资源分配问题
在资源分配问题中,如果资源量是连续变化的,这就是连续的一维资源分配问题。
设有数量为s1的某种资源,可投入A和B两种生产。第一年中以数量u1投入生产A,剩下的量s1-u1则投入生产B,年度所得收入为g(u1)=h(s1-u1),其中g(u1)和h1(u1)为已知函数,且g(0)=h(0)=0。这种资源在投入A,B生产后,年终还可以回收再用于下一年的生产。设年回收率分别0<a<1和0<b<1,则在第一年生产后,回收的资源量为s2=a1u1+b(s1-u1)。第二年资源数量s2中的u1和s2-u2分别再投入A,B两种生产,则第二年可得收入为g(u2)+h(s2-u2)。如此持续进行n年。那么,应当如何分配每年投入A生产的资源量u1,u2,···,un以使得n年的总收入最大?
由于这类问题具有明显的阶段性特征,而且各阶段(年度)之间相互联系,适合用动态规划的方法进行求解。
设sk为状态变量,表示在第k阶段初可投入A,B两种生产的资源量,uk为决策变量,它表示在第k阶段中用于A生产的资源量,则sk-uk为用于B生产的资源量,且0≤uk≤sk。状态转移方程为
![]()
设最优值函数为fk(sk),它表示从第k阶段至第n阶段采取最优分配方案进行生产后所得到的最大总收入。由此可以得到该问题的动态规划基本方程为
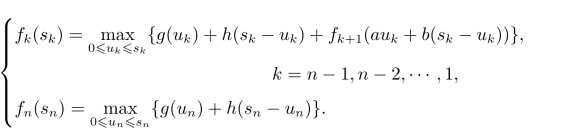
例5.7(连续的一维资源分配问题)某工厂购进100台机器,准备生产A,B两种产品。若生产产品A,每台机器每年可收入45万元,损坏率为65%;若生产产品B,每台机器每年收入为35万元,损坏率为35%。估计三年后将有新机器出现,旧的机器将全部淘汰。试问每年应如何安排生产,使三年后的总收入最大?
解将三年划分为三个阶段,即k=1,2,3。设sk为第k年初所拥有的完好机器数量,xk为第k年中用于生产产品A的机器数量,则用于产品B的机器数量为sk-xk,故可以得到0≤xk≤sk,状态转移方程为
![]()
设第k年工厂收入为dk(sk,xk),则
![]()
令fk(sk)为最优值函数,它表示从第k年到第3年末采取最优策略时工厂的最大收益,这样可以得到该问题的基本方程为

当k=3时,有
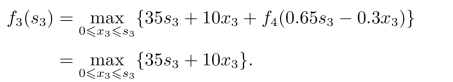
由于f3(s3)是关于x3的单调增函数,而0≤x3≤s3,所以得到
![]()
当k=2时,有

由于f2(s2)是关于x2的单调减函数,而0≤x2≤s2,所以得到
![]()
当k=1时,有

由于f1(s1)是关于x1的单调减函数,而0≤x1≤s1,所以得到
![]()
由于s1=100,所以得到该工厂的三年生产计划为
![]()
即在第一、第二年将所有机器投入产品B的生产,最后一年将所有机器投入产品A的生产,这样所获最大收益为
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






