动态规划的思想可以应用于求解一些较为一般化的优化问题。
例5.4利用动态规划思想求解下述整数规划问题的最优解:

解(1)建立动态规划模型。
阶段变量:将给每一个变量xi赋值看做一个阶段,划分为3个阶段,阶段变量k=1,2,3。
设状态变量sk表示从第k阶段到第3阶段约束右端最大值,则
![]()
设决策变量xk表示从第k阶段赋给变量xk的值(k=1,2,3),则状态转移方程为
![]()
阶段指标为
![]()
基本方程为

其中a1=3,a2=4,a3=5,[x]表示不超过x的最大整数。
(2)用逆序法求解。当k=3时,

由于s3={0,1,2,···,10},所以当s3=0,1,2,3,4时,x3=0;当s3=5,6,7,8,9时,x3可取0或1;当s3=10时,x3可取0,1,2,由此确定f3(s3),如表5.1所示。
表5.1

当k=2时,有
![]() (https://www.daowen.com)
(https://www.daowen.com)
当s2=0,1,2,3时,x2=0;当s2=4,5,6,7时,x2=0或1;当s2=8,9,10时,x2=0,1,2。由此确定f2(s2),如表5.2所示。
表5.2

当k=1时,有
![]()
由于s1=10,所以x1可取0,1,2,3,由此确定f1(s1),如表5.3所示。
表5.3

按计算顺序反推,可得最优解为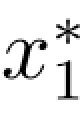 =2,
=2,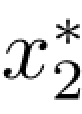 =1,
=1, =0,max z=13。
=0,max z=13。
例5.5用动态规划方法求解下述非线性规划问题:

解把依次给变量x1,x2,x3赋值的过程看做各个阶段,则该问题可划分为三个阶段,即k=1,2,3。状态变量sk表示从第k阶段到第3阶段约束右端的最大值,因此s1=12。决策变量xk表示第k阶段赋给xk的值,允许决策集合为
![]()
状态转移方程为s2=s1-x1,s3=s2-3x2;阶段指标为vk(sk,xk)=kxk;基本方程为
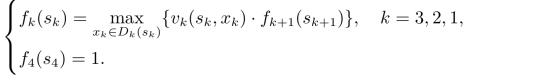
当k=3时,

与前类似,利用一阶导数条件,得到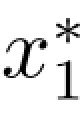 =4,f1(s1)=64。
=4,f1(s1)=64。
根据计算过程反推,得到该问题的最优解为
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








