动态规划(dynamic programming)是运筹学的一个分支，是求解多阶段决策过程最优化的数学方法。20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。1957年出版了他的名著Dynamic Programming，这是该领域的第一本著作。

动态规划问世以来，在经济管理、生产调度、工程技术和最优控制等方面得到了广泛的应用。例如最短路线、库存管理、资源分配、设备更新、排序、装载等问题，用动态规划方法比用其他方法求解更为方便。

在生产与管理实际中，有一类活动的过程，由于它的特殊性，可将过程分为若干个互相联系的阶段，在它的每一个阶段都需要作出决策，从而使整个过程达到最好的活动效果。因此，各个阶段的选取不是任意确定的，它依赖于当前面临的状态，又影响以后的发展。当各个阶段决策确定后，就组成了一个决策的序列，因而也就决策了整个过程的一条活动路线。这种把一个问题看做是一个前后关联具有链状结构的多阶段过程（如图5-1所示）称为

多阶段决策过程，这种问题称为多阶段决策问题。

图5-1　多阶段决策过程示意图

在多阶段决策问题中，阶段的划分一般说来与时间有关，决策依赖于当前的状态，阶段决策一旦作出随即影响状态的变化，对下一阶段的状态产生影响，一个决策序列就是在变化的状态中产生出来的，所以从整个决策过程来看是一个动态的过程。因此，把处理多阶段决策问题的方法称为动态规划方法。一些与时间没有关系的问题，只要人为地引进“时间”因素，也可转化为多阶段决策问题，用动态规划的方法来处理。

下面通过一些典型的多阶段决策问题来说明动态规划的基本概念。

例5.1(背包问题)有一个人带一个背包上山，其可携带物品重量的限度为a千克。设有n种物品可供他选择装入背包中。已知第i种物品每件重量为wi千克，在上山过程中的作用（价值）是携带数量xi的函数ci(xi)。问此人应如何选择携带物品（各几件）以使得所起作用（总价值）最大？

这就是著名的背包问题，类似的问题有工厂里的下料问题、运输中的货物装载问题、卫星内的物品装载问题等。

例5.2(机器负荷分配问题)某种机器可以在高、低两种不同的负荷下进行生产。在高负荷下进行生产时，产品的年产量h和投入生产的机器数量u的关系为h=h(u)。这时机器的年完好率为a，即如果年初完好机器的数量为u，到年终时完好的机器数量就是au，0<a<1。在低负荷下生产时，产品的年产量l与投入生产的机器数量v的关系为l=l(v)，相应的机器年完好率为b，0<b<1。

假定开始生产时完好的机器数量为s，要求制定一个5年计划，在每年开始时决定如何重新分配完好的机器在两种不同的负荷下生产的数量，使5年内产品的总产量达到最高。(www.daowen.com)

这类问题本质上是资源的合理调配问题，在管理实际中广泛存在。

例5.3(最短路线问题)如图5-2所示为一个线路网络，两点之间连线上的数字表示两点间的距离（或费用）。试求一条由As到Gt的铺管线路，使总距离为最短（或总费用最小）。

在图5-2中，从As到Gt铺设管线可以划分为6个阶段：

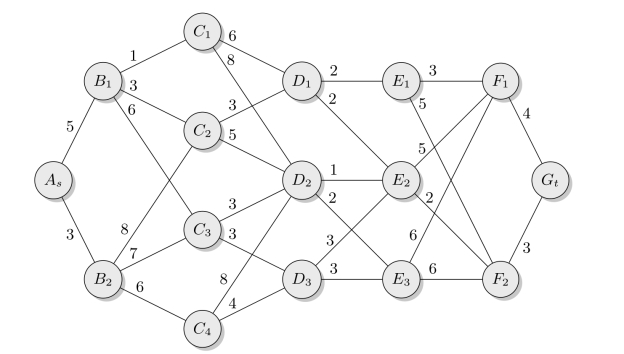
图5-2　最短路线问题

第一阶段（As→Bi）As为起点，B1,B2为终点，因而这时走的路线有两个选择，走到B1或B2。

第二阶段（Bi→Cj）若上一阶段的决策为B1，则现在有三条线路可供选择，走到C1,C2或C3；若上一阶段的决策为B2，则现在也有三条线路可供选择，走到C2,C3或C4。

第三阶段（Ci→Dj）若上一阶段的决策为C1，则现在有两条线路可供选择，走到D1或D2；若上一阶段的决策为C2，则现在有两条线路可供选择，走到D1或D2；若上一阶段的决策为C3，则现在有两条线路可供选择，走到D2或D3；若上一阶段的决策为C4，则现在有两条线路可供选择，走到D2或D3。

第四阶段（Di→Ej）若上一阶段的决策为D1，则现在有两条线路可供选择，走到E1或E2；若上一阶段的决策为D2，则现在有两条线路可供选择，走到E2或E3；若上一阶段的决策为D3，则现在有两条线路可供选择，走到E2或E3。

第五阶段（Ei→Fj）若上一阶段的决策为E1，则现在有两条线路可供选择，走到F1或F2；若上一阶段的决策为E2，则现在有两条线路可供选择，走到F1或F2；若上一阶段的决策为E3，则现在有两条线路可供选择，走到F1或F2。

第六阶段（Fi→Gt）无论上一阶段的决策为F1或F2，则现在只有一条线路可供选择，直接走到Gt。

从上述分析可以发现，不同阶段的决策依赖于当前的状态，同时也影响下一阶段决策的状态，各个决策阶段通过状态的变化联系起来。另外，不同线路的选择使得最终的线路长度也不一样。上述过程实质上是一种枚举的方法，整个过程中共包括了48条不同线路，计算出不同线路的长度，即可得到最短线路。这样的计算过程显然是繁琐的，当阶段数、节点数增多以后，计算量急剧上升。所以这样的枚举方法是不合适的，但通过上述过程可以帮助我们进一步理解多阶段决策问题的特点。