与线性规划的图解法类似，对于只有两个决策变量的目标规划问题可以利用图解的方式进行求解。如前述的目标规划问题：

图4-1　目标规划图解法（一）

例4.2某手机厂装配A,B两种型号的手机，每装配一部手机需占用装配线1小时，装配线每周计划开动40小时。预计市场上A型手机的销量是24部，每部可获利80元；B型手机的销量为30部，每部可获利40元。该厂确定的目标如下：

第一优先级：充分利用装配线每周计划开动的40小时；

第二优先级：装配线加班，但加班时间每周尽量不超过10小时；(www.daowen.com)

第三优先级：装配手机的数量要尽量满足市场需要，因A型手机利润高，取其权系数为2。

试建立该问题的目标规划模型，并求解。

解设x1,x2分别为A,B两种型号手机的产量。根据问题要求可以得到如下的目标规划模型：

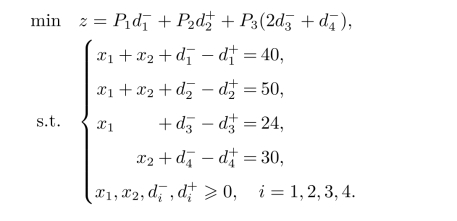
该模型的图解过程见图4-2。

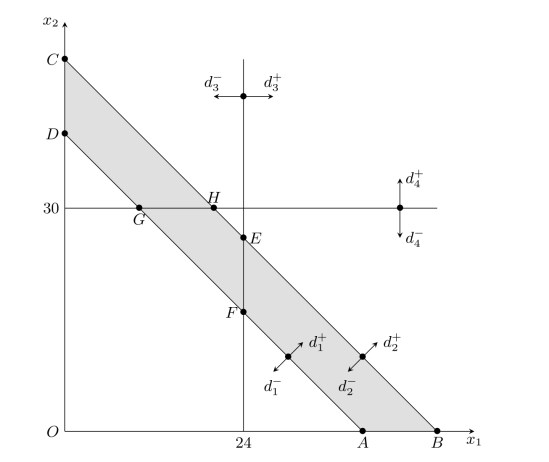
图4-2　目标规划图解法（二）

由图4-2可知，在考虑具有P1和P2优先级的目标实现后，x1和x2的取值范围为ABCD。考虑P3级的目标要求时，因d-3的权系数大于d-4的，所以先取d-3=0，这时x1和x2的取值范围为ABEF。在ABEF中只有E点使d-4取值最小，所以取E点为满意解，其坐标为(24,26)。