前面接触到的优化问题都只有一个目标，如利润最大或成本最小。但在实际的管理过程中，会有很多的多目标问题。如企业在追求最大的经济效益时，同时可能还需要兼顾社会效益、公众形象等多个方面的需求。目标规划是解决存在多个目标的最优问题的基本方法，它把多目标决策问题转化为线性规划来求解，在现实中有着十分广泛的应用。

例4.1(目标规划)某企业生产A,B两种产品，已知相关数据如表4.1所示。试确定企业利润最大化的生产方案。

表4.1　产品的生产参数

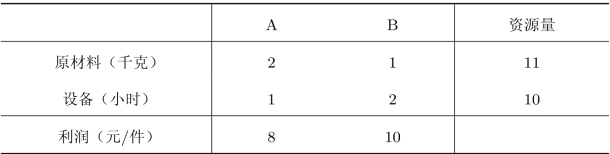
解这是一个典型的单目标规划问题，可以利用线性规划进行求解。假设A,B两种产品的产量分别为x1和x2，则可得到如下的线性规划模型：

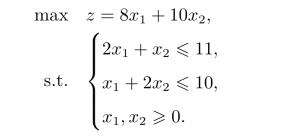
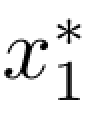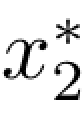求解得到问题的最优解为=4，=3；企业的最大利润为max z=62元。

如果企业在作决策时还要考虑市场等一系列的其他条件，如：

(1)根据市场信息，产品A的销售量有下降的趋势，所以要求产品A的产量不大于产品B的产量；

(2)超过计划供应的原材料时，需要高价采购，但会成本增加；

(3)应尽可能充分利用设备台时，但不希望加班；

(4)应尽可能达到并超过计划利润指标56元，

这样在考虑产品决策时，就成为多目标决策问题。目标规划方法是解决这类决策问题的基本方法之一。在建立目标规划模型的过程中，需要用到一些特有的概念，现简要介绍如下：

1.正、负偏差变量d+和d-

正偏差变量d+表示决策值超过目标的部分；负偏差变量d-表示决策值未达到目标值的部分。因决策值不可能既超过目标同时又未达到目标，所以d+×d-=0总是成立的。

2.绝对约束和目标约束

绝对约束是指必须严格满足的等式约束和不等式约束；如线性规划问题的所有约束条件，不能满足这些约束条件的解为非可行解，所以这些约束都是绝对约束。目标约束是目标规划所特有的，可把约束右端项看做是要追求的目标值，在达到该目标值时允许发生正或负偏差，因此在这些加入正、负偏差变量的约束都是目标约束。线性规划问题的目标函数在约定目标和加入正、负偏差变量后可变换为目标约束，也可根据问题的需要将绝对约束变换为目标约束。如在例4.1的目标函数z=8x1+10x2中，若要求尽可能达到并超过计划利润指标56元，则可转换为目标约束8x1+10x2+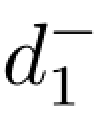-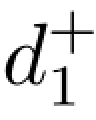=56；绝对约束2x1+x2≤11可变换为目标约束2x1+x2+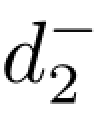-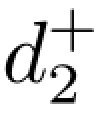=11。(www.daowen.com)

3.优先因子（优先等级）与权系数

目标规划问题有多个目标，但决策者在要求达到这些目标时，是有主次或轻重缓急的不同。在目标规划中，约定要求第一位达到的目标赋予优先因子P1，第二位达到的目标赋予优先因子P2······并要求

表示Pk比Pk+1具有更大的优先权。即在优化时应首先保证P1级目标的实现，这时可不考虑次级目标；而P2级目标是在实现P1级目标的基础上才考虑的；以此类推，若区别具有相同优先因子的两个目标的差别，这时可分别赋予它们不同的权系数wj。

4.目标规划的目标函数

目标规划的目标函数（也称为准则函数）是按各目标约束的正、负偏差变量和赋予相应的优先因子而构造的。当每一目标值确定后，决策者的要求是尽可能缩小偏离目标值，因此目标规划的目标函数只能是

通常它具有三种基本形式：

(1)要求恰好达到目标值，即正、负偏差变量都要尽可能地小，这时有

(2)要求不超过目标值，即允许达不到目标值，也就是正偏差变量要尽可能地小，这时有min z=f(d+)。

(3)要求超过目标值，即超过量不限，但必须是负偏差变量要尽可能地小，这时有min z=f(d-)。

对每一个具体的目标规划问题，可根据决策者的要求和赋予各目标的优先因子来构造目标函数。

如在例4.1中，决策者在原材料供应受严格限制的基础上还需考虑：首先是产品B的产量不低于产品A的产量；其次是充分利用设备有效台时，不加班；再次是利润额不小于56元。按决策者的要求，分别赋予这三个目标P1,P2,P3优先因子，得到如下目标规划模型：

更一般地，目标规划的数学模型可以描述为