下面我们通过一些案例来说明整数规划问题在现实中的应用。

案例一教材出版优化

ABC出版公司是一家小型大学课本出版公司，它目前需要对来年将出版的教材科目做出决策。表3.8为考虑出版的书籍和对应书籍3年中的预期销售量。表3.8中被列为修订本的书是已经与公司签订合同的，列为新书的书只是已由公司审阅过，但是还未签订合同。该公司现有3人可以接受这些任务。他们的可用时间不同，甲有60天可用，乙与丙都有40天可用时间。每个人完成每项任务需要的天数在表3.9中列出。

表3.8　ABC出版公司对出版书籍的预期

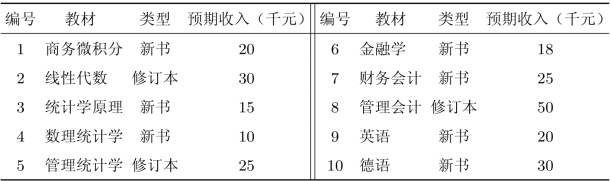
表3.9　甲、乙、丙三人完成每项任务需要的天数

表3.9表示，如果要出版商务微积分需要30天甲的时间和40天乙的时间，“—”表示此任务不需要此人。ABC公司在一年中不会出版两本以上统计学的书和一本以上会计学的书。而且，已决定必须在两本数学书（商务微积分和线性代数）中出版一本，但不会都出版。

现根据上述信息和相关要求确定ABC公司的出版计划，以使公司的预期销售收入最大，并确定相关人员的安排。

分析与建模计划中共有10本教材需要出版，对每本教材而言是要确定其是否出版，所以可以引入0-1型变量对其进行描述。假设

为了描述方便，假设第j本书的预期收入为rj，不同人i花费在不同教材j上的时间为cij，i=甲,乙,丙，j=1,2,···,10，则公司的目标函数为

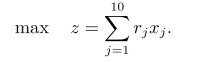
此外，由于必须在两本数学书（商务微积分和线性代数）中出版一本，但不会都出版，所以

已知不出版两本以上统计学的教材，所以

已知不出版一本以上的会计学的教材，所以

另外，对于三位工作人员的时间有一定的限制，即对甲、乙、丙分别存在

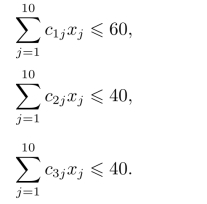
将上述目标函数和约束条件整合到一起，可以得到如下0-1整数规划模型：

利用Excel或LINGO软件求解上述优化模型后得到x2=x4=x5=1，其他为0；z∗=65。即公司只需要出版：线性代数、数理统计学和管理统计学3本教材。

案例二飞行计划安排

某航空公司经营A,B,C三个城市间的航线，这些航线每天班机起飞与到达时间如表3.10所示。

表3.10　班机起飞与到达时间

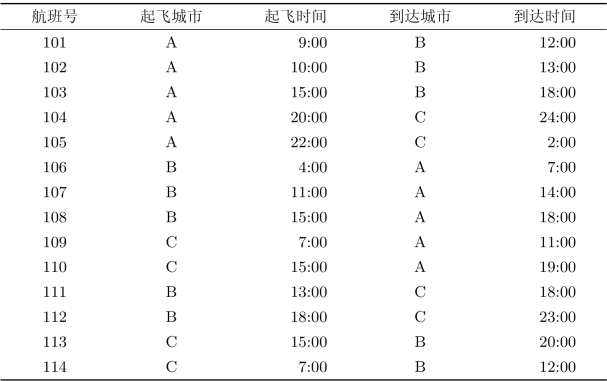
设飞机在机场停留的损失费用与停留时间的平方成正比，又每架飞机从降落到下班起飞至少需要2小时的准备时间。根据上述信息确定公司停留费用损失最小的飞行方案。

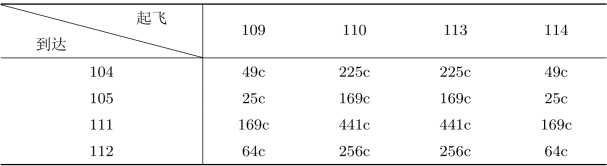
分析与建模注意到对于每个城市而言，其进出港航班的数量是相等的，所以所有飞机都是执行的往返飞行任务。这样，可以把从某城市起飞的飞机当做要完成的任务，到达的飞机看做分配去完成任务的人，只要飞机到达后两小时，就可分配去完成起飞的任务。这样可以分别针对城市A,B,C建立起一个指派问题。各指派问题的效率矩阵为飞机停留的损失费用，假设飞机每停留1小时的损失为c元，停留时间为t小时，则停留损失为ct2元。由此可得到3个城市指派问题的效率矩阵分别如表3.11～表3.13所示。

表3.11　城市A

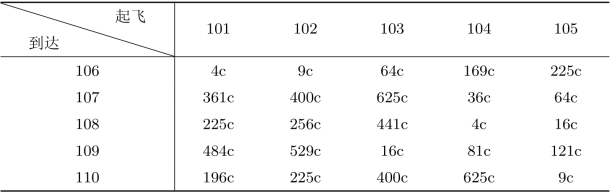
表3.12　城市B

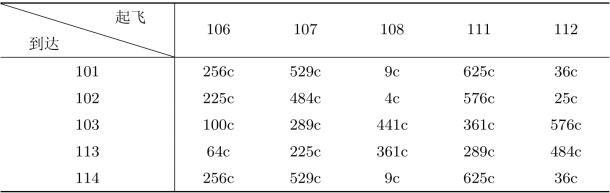
表3.13　城市C(www.daowen.com)

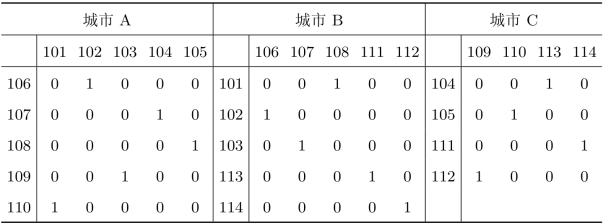
利用匈牙利法对上述三个指派问题进行求解后即可得到最优的指派计划如表3.14所示。

表3.14　最优化结果

案例三设备更新选择优化

某电线厂生产2种规格的裸铜线和2种规格的塑包线，塑包线的钢丝直径同相应规格的裸铜线。其生产工艺流程如图3-9所示。由于市场需求扩大及某些设备比较陈旧，计划拟新增或改造现有某种设备，有关方案及相应设备费用及生产率有关数据如表3.15所示。双市场对各种规格电线的年需求量如表3.16所示。试确定满足市场需求，并使运行等各种费用（新购及改造设备按每5%提取折旧费，老设备不提）为最小的方案。

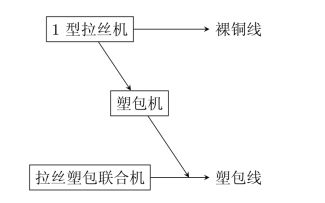
图3-9　生产工艺流程

分析与建模用Mi表示第i种型号机器的数目，用xij表示第i种型号机器用于生产第j种规格线材所占的时间比例（i=1,2,···,5，j=1,2）。

目标函数是使新购及改造设备的年折旧（0.05K）、设备年固定费用（F）、年运行费用（R）和废品损失（L）四项的总和为最小，即

表3.15　案例三的数据

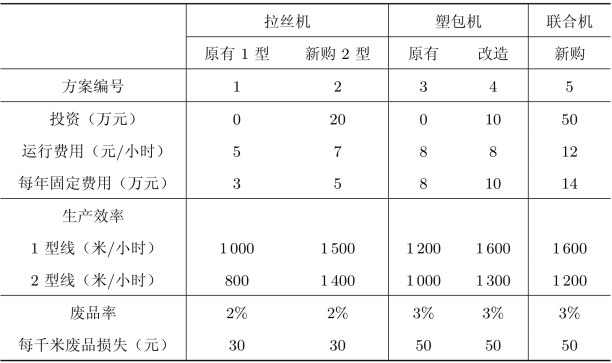
表3.16　年需求量

其中，

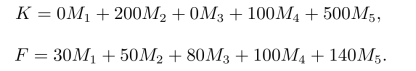
设每台设备年运行6 000小时，则设备1的年运行费用为30(x11+x12)千元，类似地可算出设备的运行费用，由此可得

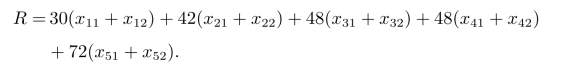
设备1造成的废品损失为

类似地可得到其他设备的废品损失，故有

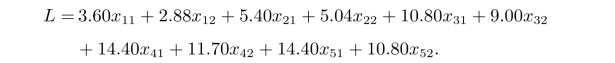
问题的约束条件分为以下几类：

(1)满足市场需求：对裸铜线（规格1）不仅直接满足市场需求，而且需作为塑包线（规格1）的半成品，所裸铜线（规格1）的需求量为

裸铜线（规格1）由设备1和设备2生产，考虑废品损失有

由此可写出满足市场需求的约束有

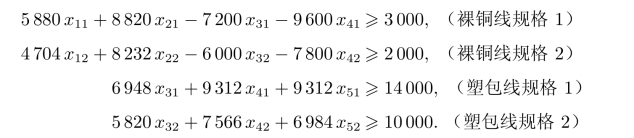
(2)机器生产能力约束

(3)原生产线设备数的约束

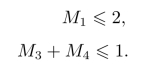
根据上述目标函数与约束条件即可得到该问题的整数规划，求解后得到问题的最优解，此外略去这一过程，请大家自行利用相关软件进行求解。