指派问题（Assignment Problem）是生活中经常遇到的问题。其基本描述为：现有n项工作需要完成，正好有n个人可以承担这些工作。由于每个人的专长不同，各人完成不同工作的耗费也不同，于是产生这样一个问题：如果要求每个人只能承担一项工作，而且每项工作也只能由一个人完成，应指派哪个人去完成哪项工作，使完成n项工作的总耗费最少。

假设某人i完成某项工作j的耗费为cij，i=1,2,···,n，j=1,2,···,n，则由cij可构成一效率矩阵C，

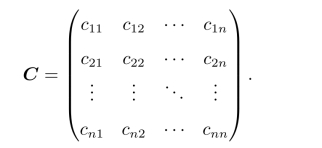
由于指派问题要求某人只能承担一项工作，所以对该人而言指派结果只有两种可能：要么被指派给了某工作，如k，要么就没有指派给工作k，而且这两种可能是相互矛盾、非此即彼的情况。从工作的角度也是这样，某项工作要么指派给了某人，要么没有。所以，对于这种相互矛盾、非此即彼的选择问题可以使用0-1变量来进行描述。即设

根据指派问题的要求，可以得到如下指派问题的数学模型：

该模型中，第一个约束条件表示对于某项工作j而言，只能由1人承担，第二个约束条件表示对于某人i而言，只能承担1项工作。由此可以发现，指派问题的可行解应该满足这样的条件：在由xij所构成的0-1矩阵中，每一行只能有一个1，每一列也只能有一个1。所以指派问题本质上是一个组合优化问题，只需要确定这n个1的位置以使得总的耗费最小。

求解指派问题的方法叫做匈牙利法，是库恩（W.W.Kuhn）在1955年提出的。在指派问题的求解过程中，使用了匈牙利数学家康尼格（D.König）一个关于效率矩阵中0元素的定理：效率矩阵中独立0元素的最多个数等于能覆盖所有0元素的最少直线数。下面我们以一个实例来说明匈牙利法求解指派问题的思路与过程。

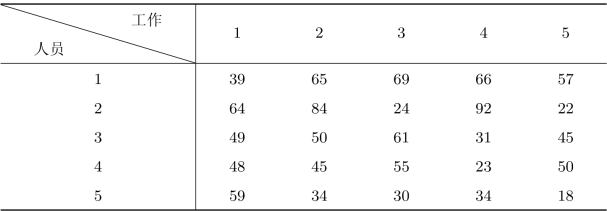
例3.3(指派问题)某企业要有5项工作需要展开，同时有5个人员可胜任这些工作，每个人完成不同工作所耗费的时间如表3.4所示。试确定一个最优方案，使得完成这5项工作花费的时间最少。

对于指派问题，容易想到的是让每个人都承担自己最擅长的工作，每项工作都由最擅长的人来承担是耗费最小的一种最优指派方案。如在这个问题中，最好应该指派第1个人去完成工作1，第2个人去完成工作5······或者从工作的角度而言，最好应该指派工作1给第1个人，指派工作2给第5个人······如果能按这种方式指派成功（达到约束条件的要求），得到的自然是最优指派。但是，通常情况下这种指派方式会发生冲突，如在该问题中第2人和第5人都最擅长工作5。所以，这种情况下上述方法是行不通的。但是我们可以发现，在确定最优指派时我们关注的是效率的相对值（因为最小值是一个相对的概念），而且前面也提到指派问题是一个组合优化问题，即我们不关注效率的绝对值，而是关注这些效率值的相对大小。所以，为了更清楚反映出这些效率值之间的相对关系，首先将效率矩阵的各行减去该行的最小值，然后再将效率矩阵的各列减去该列的最小值，得到如下矩阵：

表3.4　指派问题的效率矩阵

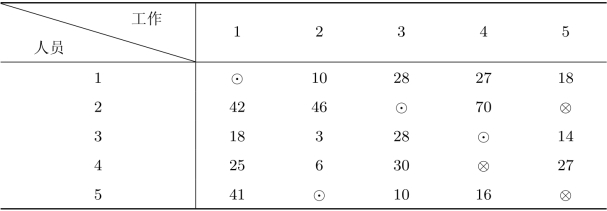
可以发现，在矩阵B1中存在着一些0元素，这些0元素所在位置要么表示某人最擅长的工作，要么表示某工作谁最擅长。所以，最优指派方案应该选择这些0元素所在位置进行指派。这里涉及前面提到独立0元素的概念，它是指在某一行或在某一列只有一个0元素，则该0元素称为独立0元素。独立0元素在指派问题中有着重要作用，它表示相对来说某人只擅长一项工作或者某项工作只有一人擅长，所以在指派时首先应该考虑按独立0元素来进行指派。如矩阵B1中，(1,1)位置的0无论从行或者列来看都是独立的，(2,3)位置的0元素从行来看是不独立的，但从列来看却是独立的，所以它也是独立0元素。

下面我们按独立0元素进行指派。指派过程中首先按行检查独立0元素所在位置，并进行指派，然后再按列进行指派，一直重复这一过程直到没有独立0元素为止。但在这个过程中，要注意如果按行（列）找到了一个独立0元素并进行了指派，就应该删除该独立0元素所在列（行）的其他0元素。如按行查找时，第三行有一个独立0元素，即应指派第3个人去完成第4项工作，自然第4项工作就不能再由其他人来承担，所以应该删除第4列的其他0元素，即位置(4,4)的0元素。我们用⊙表示指派成功的点，用⊗表示被删除的0元素，得到如表3.5所示的指派方案。

表3.5　指派问题的求解过程（一）

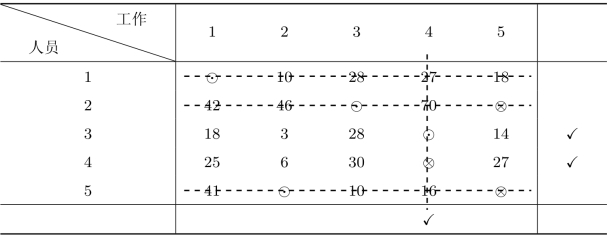
在表3.5所示的结果中，只存在着4个指派点，剩下第4个人和第5项工作没有指派。那么，是不是直接指派第4个人去完成第5项工作就行了呢？这显然不是好的指派方案，这一方案需要增加总的时间27。但如果指派第4个人承担工作4，第3个人承担工作2，第5个人承担工作5，只需增加3单位时间即可。尽管这一方案不一定是最优的，但它比直接指派第4个人去完成第5项工作的方案更优。产生指派不成功的原因在于：无论从人或工作的角度按最擅长进行指派存在冲突，即上述矩阵B1中的独立0元素个数（4个）是少于工作数（5个）的。这样，按最擅长来考虑这一指派问题是没有办法指派成功的，所以必须考虑次擅长因素，即要从全局的角度考虑某人或某项工作的第二擅长因素。更直观地讲，当前指派没有成功是因为矩阵B1中的独立0元素不足而造成的，为了指派成功需要考虑次擅长因素的情况下增加一些0元素。但是在这一过程中，需要将原有的0元素（最擅长因素下）“保护”起来的情况下增加0元素。具体过程如下：(www.daowen.com)

(1)对未指派成功的行作标记“√”。

(2)对已作标记的行所有含“⊗”元素的列作标记“√”。

(3)对已作标记的列中含有“⊙”元素的行作标记“√”。

(4)重复(2),(3)，直到得不到新作标记的行或列为止。

(5)用直线划掉没作标记的行和作标记的列，所得到的直线数即为覆盖所有0元素的最小直线数。如果该数小于矩阵维数，则指派不能成功；如果该直线数等于矩阵维数，则能指派成功。

按此过程，该问题的标记结果如表3.6所示。

表3.6　指派问题的求解过程（二）

.接下来，增加0元素。首先在未被划掉的元素中选择最小元素（(3,2)位置的3），然后作标记的行减去这一最小元素，作标记的列加上这一最小元素，得到考虑了次擅长因素的新效率矩阵B2，如下：

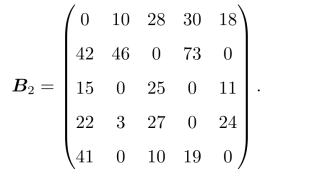
再按前述指派方法进行指派，得到如表3.7所示指派结果。

表3.7　指派问题的求解过程（三）

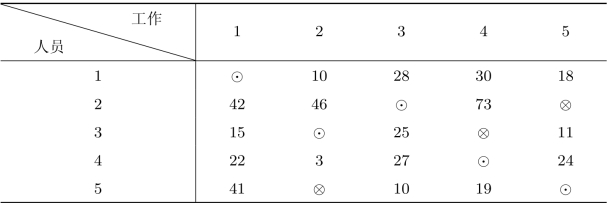
在表3.7中，共有5个指派点，所以指派成功，最优指派为：人1—工作1，人2—工作3，人3—工作2，人4—工作4，人5—工作5，所需总时间为z∗=154。

上述利用匈牙利法求解指派问题的过程需要注意：

(1)指派问题要求目标函数为最小化，且人数与工作数相等。所以在求解指派问题时，如果这些条件不能得到满足，首先应作相应处理，具体处理方法可参考运输问题的处理方法。

(2)指派问题的求解过程是行列对称的算法，所以在求解过程中既可以按先行后列进行，也可以按先列后行进行，对最优结果不产生影响。

(3)指派问题不会存在无可行解的情况，但是可能会产生非唯一解的情况。在求解过程中，可能会遇到由于0元素过多，造成每一行、每一列都不止一个0元素时（这意味着存在多个最优指派方案），可以将某行或某列的其中一个0元素假定为独立0元素处理，再按前述方法进行指派，即可得到问题的一个指派方案。