割平面法的基本思路仍然是利用解线性规划来求解整数规划。其基本求解过程为：首先不考虑整数规划问题的整数要求，利用单纯形法求解，得到问题的最优解，若满足整数要求则停止；否则，在最优单纯形表的基础上，考虑整数要求，增加整数约束条件（即割平面），将可行域切割掉一部分，而且被切去的部分只包含非整数解，没有切割掉任何整数可行解。然后再利用单纯形法继续求解增加约束条件的线性规划问题，得到新解后重复上述过程，直到切割后的可行域的一个整数坐标的极点恰好是问题的最优解。所以，割平面法的关键是在如何构造割平面。

例3.2(整数规划问题的割平面法)求解如下整数规划问题:

解首先不考虑问题的整数要求，求解其对应的线性规划问题，得到表3.1所示的最优单纯形表，图3-5反映了问题的可行域与最优解情况。

表3.1　最优单纯形表

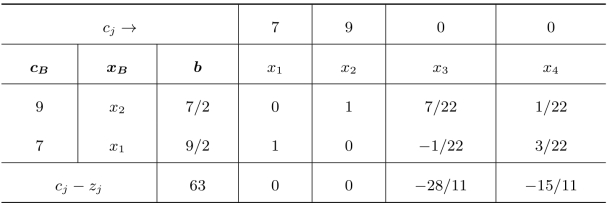
图3-5　割平面法（一）

由表3.1可知，当前问题的最优解不满足整数要求。为了反映出整数要求，我们选择当前解中非整数解的变量x2（也可选择x1）所在的行进行变化，根据最优单纯形表有

为了反映出问题的整数要求，将上述变量之间的关系式按下述要求进行变换：将系数与常数项都分解成整数和非负真分数之和，然后移项后得到

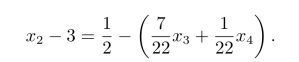
由于上式左端为两个整数的差，而等式右端为一个真分数减去某个数的差，所以存在

且

此约束条件即为要求变量x2为整数时，对相关变量的约束。并且有x2-3=-s1，以及x2≤3，此即为找到第一个割平面，如图3-6所示。

将上述约束条件加入前面的最优单纯形表中，并使用对偶单纯形法求解，如表3.2所示。

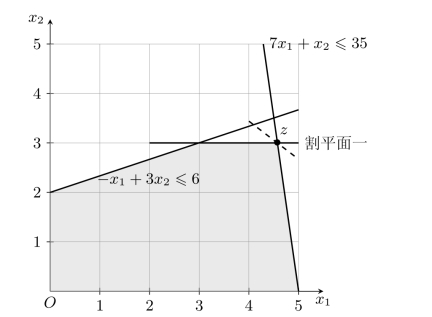
图3-6　割平面法（二）

表3.2　最优单纯形表

(www.daowen.com)

由表3.2可知，x1仍然是非整数解，根据表3.2中x1所在行可以得到

整理得到

即

以及x1-s1≤4。又由于x2-3=-s1，所以x1+x2≤7，此为第二个割平面（如图3-7）。再将上式约束加到前面最优单纯形表中，利用对偶单纯形法求解，如表3.3所示。

图3-7　割平面法（三）

表3.3　最优单纯形表

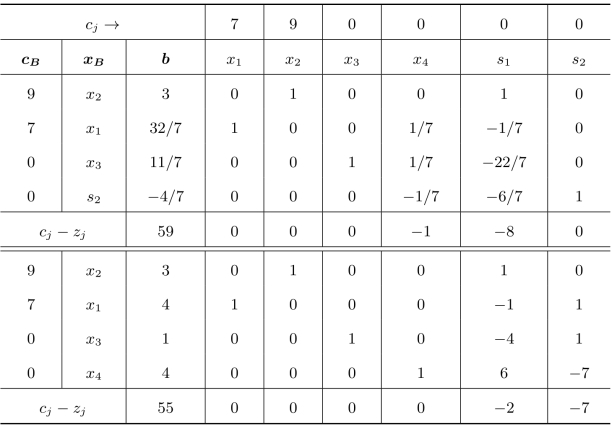
由此得到该问题的最优解为

上述即为割平面求解整数规划问题过程，现总结如下：

(1)令xi是相应线性规划问题最优解中的非整数解的基变量，根据最优单纯形表可以得到

其中i∈B，B为基变量下标的集合；k∈N，N为非基变量下标的集合。

(2)将bi和aik都分解成整数部分N和非负真分数f之和，即

代入(3.4)后，得到

(4)重复上述过程，直至得到问题的整数最优解。