如前所述，如果整数规划问题对应的线性规划问题的可行域有界，则整数规划问题的可行解是可数的，但对于一些复杂的整数规划问题，枚举法面临着巨大的计算量，使其无法成为求解整数规划问题的一般方法。

分支定界法的基本思想是拆分排除法。对于那些很难直接处理的大问题，可以把它拆分成越来越小的子问题，直到这些子问题能被处理。拆分（分支）的工作是通过把整个可行解的集合分成越来越小的子集来完成的，排除（剪枝）的工作是通过界定子集中的最好的解接近最优解的程度，然后舍弃离最优解越远的子集来实现的。

例3.1(整数规划的分支定界解法)利用分支定界法求解下列整数规划问题：

解先不考虑该问题的整数约束，求解其对应的线性规划问题，容易得到最优解为

如图3-2所示。可见该解不符合整数要求，这时z0可看做该整数规划问题最优目标函数值的上界¯z。另外可以任选一个整数规划问题的可行解，如x1=x2=0，这时得到z=0，将其作为整数规划问题最优解的下界，即

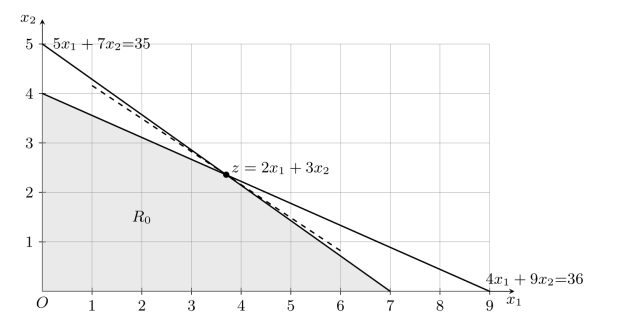
图3-2　分支定界法（一）

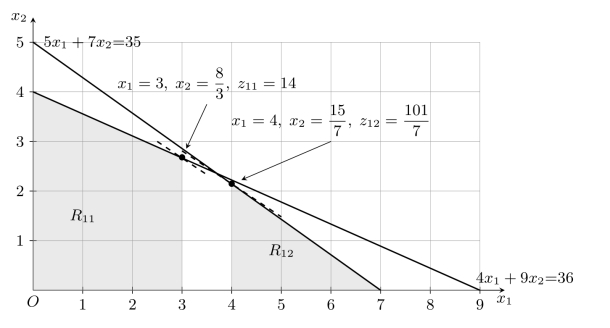
同时将原可行域R0也对应地划分为两个区域R11和R12，如图3-3所示。

(www.daowen.com)

图3-3　分支定界法（二）

分别求解问题B11和问题B12，可以得到其最优解分别为

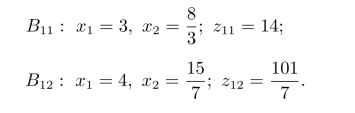
得到的解仍然不满足整数约束条件，但存在z∗≤max{z11,z12}，所以修改z∗的上界，得到

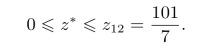
接下来重复上述步骤，对B11问题分别添加约束条件x2≤2和x2≥3得到新的两个分支B111和B112，即R11区域划分为R111和R112两个可行域，如图3-4所示。

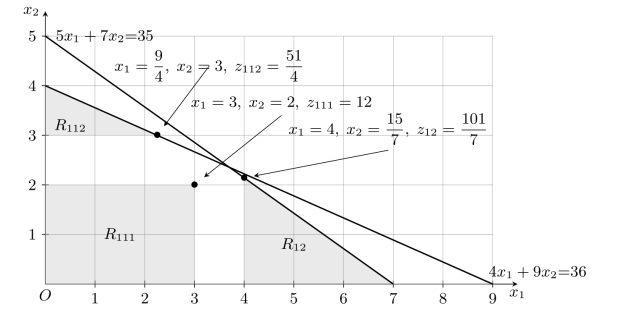
图3-4　分支定界法（三）

求解问题B111和问题B112分别得到最优解为

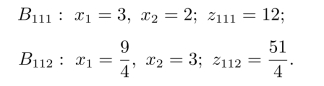
由于B111得到了整数可行解，所以可修改z∗的下界，而B112得到的仍然是非整数解，所以修改z∗的上界，但在区域R111∪R112∪R12中，由于z112<z12，所以得到

一直重复上述过程，对问题的可行域不断进行切割，去掉非整数解。求解过程中如果得到整数可行解则考虑提高z∗的下界，若得到了非整数解则考虑降低z∗的下界，直到上、下界收敛到一起，这时得到整数规划问题的最优解。对于该问题，最终可以得到问题的最优解为