整数规划问题是基于现实需要而提出的。前面讨论的线性规划问题中，并没有考虑到现实问题中许多时候对问题的解有整数要求这一条件，如需要的人数、车辆的产量等。如果一个问题与线性规划的不同之处仅在于要求变量取值为整数，那么它就是一个整数规划问题（Integer Programming，IP）。整数规划问题是在线性规划问题的基础上增加了对决策变量为整数的要求。如果只要求部分变量为整数值，则称为混合整数规划；如果要求所有变量都为整数值，则称为纯整数规划问题。

由于整数规划与线性规划之间存在着密切关联性，容易想到利用解线性规划问题的思路来求解整数规划问题。但是，如果只是单纯对线性规划求解得到的结果进行整数化处理（如取整或四舍五入），是无法保证整数规划问题的最优性的。如整数规划问题

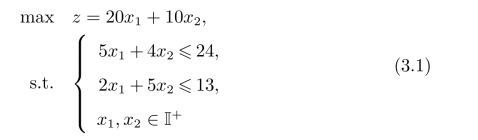
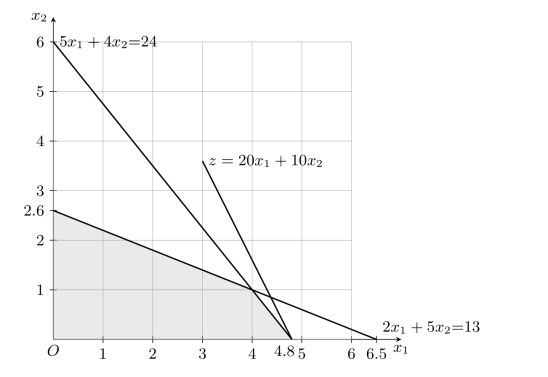
中，当不考虑其整数约束时，容易得到其最优解为

(www.daowen.com)

图3-1　整数规划问题示例

由此可见，这两种整数化处理的方法都无法确保解的最优性。尽管如此，还是可以从上述分析过程中得到如下一些对于整数规划问题的基本认识：

(1)整数规划问题对应的线性规划问题有最优解是整数规划问题有最优解的必要条件，而且当其对应的线性规划问题的最优解满足整数要求时，该解自然也是整数规划问题的最优解。

(2)对于最大化的整数规划问题，如果存在最优解，则其最优值小于或等于其对应的线性规划问题最优值。即整数规划问题的最优解可能在其对应线性规划问题可行域的内部实现。

(3)与线性规划问题相比，整数规划问题的可行解一般是有限个的。这样对于一些简单的整数规划可以依赖于枚举方法进行求解。

整数规划问题的一般解法为分支定界解法和割平面法，下面对这两种解法作一简要介绍。