案例三运输问题

某企业有3个生产基地，3个销售地，它们每月的产量和需求量如表2.32所示。

表2.32　单位运价与产销量

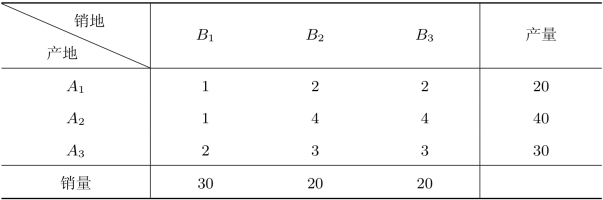
若产量大于需求量，则某些产地的产品需要留在原生产地，假设未运出的产品会产生一定存储费用，产地A1,A2,A3的单位产品存储费用分别为5,4,3。另外，企业要求产地A2的产品至少运出38个单位，产地A3的产品至少运出27个单位。试决定企业的最优调运方案。

这是一个运输问题，但是存在着许多其他额外的要求。为了使用表上作业法进行求解，需要将其转化为一个产销平衡的运输问题。首先注意到是供过于求的，所以增加一个虚拟销地B4，其销量为产销量的差额20。各个产地的产量如果运往该虚拟销地，实际上这些运输并未真实发生，而是在各个产地发生了存储，所以各个产地运往该虚拟销地的运价应为其相应的存储费用，如表2.33所示。

表2.33　运输问题的原始数据

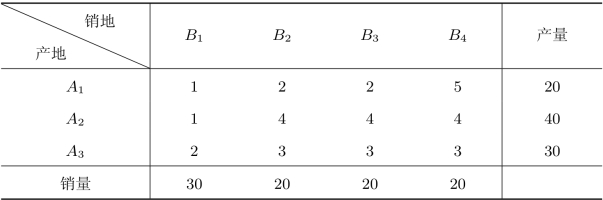
另外，由于要求产地A2的产品至少运出38个单位，则A2运出的产品中至少有38个单位是运到B1,B2,B3的，而不能是B4。所以，我们可以将A2看做两个产地A21和A22，其中A21的产量为38，它的产量必须运到B1,B2,B3，而A22的产量为2，它可以运到所有的销地。对要求产地A3的产品至少运出27个单位也可采取同样的处理方式，这样可得到如表2.34所示的产销平衡表，其中M表示任意大的正数。

表2.34　调整后的产销平衡表

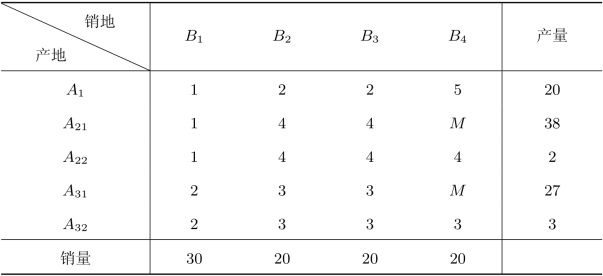
然后利用表上作业法求解，得到最优调运方案如表2.35所示。

表2.35　最优调运方案

案例四运输问题

某公司在A1,A2两地生产同一种产品，现需考虑一、二两个季度的生产计划。不同的产地、不同的季节，其生产费用和生产能力都不同。产地A1,A2两个季度的生产费用和生产能力如表2.36所示。

表2.36　生产费用和生产能力

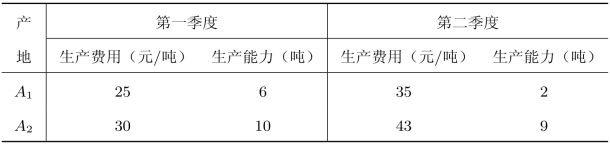
A1,A2生产的产品可以运输到两个销地B1,B2（运输时间可以不计），以满足两地的需求，B1,B2两地的需求量如表2.37所示。

表2.37　需求量(www.daowen.com)

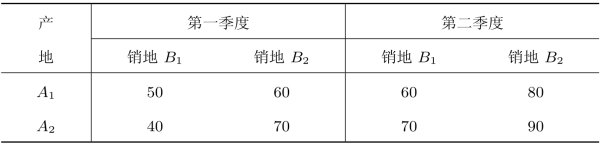
运输费用（元/吨）也随运输路线和季度不同而变化，如表2.38所示。

表2.38　运输费用

另外，每个产地和销地都可以库存第一季度的产品，以供第二季度之用，每季度库存费用（元/吨）如表2.39所示。

表2.39　库存费用

求两个季度的最优生产和库存计划，使两个季度的总费用最小。

分析与求解在该问题中，企业面临的费用来自多个方面：生产费用、运输费用和存储费用。为了方便求解，我们可以考虑将其转化为一个运输问题进行求解。

首先，由于产地A1,A2的产量不仅可用于本季度的消费，而且第一季度的产量还可用于第二季度的消费，所以可以考虑存在4个生产地；另一方面，对于两个销售地的需求量而言，第一季度必须由第一季度的产量来满足，第二季度的可以由第一季度或第二季度的供给，所以我们也将其作为4个销售地对待。

假设Aij为产地Ai第j季度的产量，Bij为销地Bi第j季度的需求量，其中i=1,2;j=1,2。下面我们考虑不同产地到不同销售地的费用问题，这里的费用包括生产费用、运输费用和存储费用。

若是当季生产当季消费，则不考虑存储费用。A11到B11的单位产品费用包括A1产地的生产费用25和运输费用50，即A11到B11的费用为75。

但是在考虑第一季度产量供第二季度消费时，需要考虑存储费用，比如A1生产供第二季度B1消费时，需考虑存储费用。若先存储在A1，第二季度再运往B1，则费用为25+2+60=87；也可以是A1第一季度生产出来后，先运输到B1，在B1存储，此时的费用为25+3+50=78。从费用最少的角度考虑，应该选择第二种方案，即A1第一季度生产出来后，先运输到B1，在B1存储，A11到B21的费用为78。

总之，按照上述分析过程，可以得到如表2.40所示的运输问题表格。

表2.40　案例四运输问题初始数据

但是形成的运输问题仍然是一个产销不平衡的运输问题，产量大于销量，所以需增加一个虚拟销地，将其转化为产销平衡问题，然后使用表上作业法求解即可。

【注释】

[1]若x1,x2,···,xn∈Rn，则这n个点的凸组合形成的区域为一个单纯形，即凸集x=αjxj为一单纯形，其中αj≥0且αj=1。如二维平面中的凸多边形为单纯形，而且只要知道该多边形顶点的坐标，就可用其顶点坐标的凸组合表示这个多边形区域。