案例一汽车装配

XYZ公司是一家汽车制造商，主要生产两种类型的汽车：中型车老虎和豪华车狮子。中型车老虎是定位于普通家庭使用的四门私家轿车，每销售一辆可为公司产生0.8万元的利润；而豪华车狮子是定位于中上层富裕家庭使用的两门私家轿车，每销售一辆可为公司产生1.5万元的利润。

公司下属的一个工厂负责组装这两种车型的汽车。每月初，该工厂需要决策该月度的生产计划。目前，该工厂本月有4800个工时可供使用，而且装配一辆老虎需要6个工时，装配一辆狮子需要10个工时。

此外，两种车型使用相同的车门。车门是由外协工厂提供的，外协工厂每月提供2 000个车门（左右车门各1 000个）。另外，公司根据市场情况对两种车型本月的需求情况进行了预测，对于老虎车型其需求没有限制，而对狮子车型的需求不会超过3 500辆。

那么，该汽车装配公司本月最优的生产计划是什么？

假设x1为老虎车型的生产量，x2为狮子车型的生产量，则根据案例提供的信息可以得到如下线性规划模型：

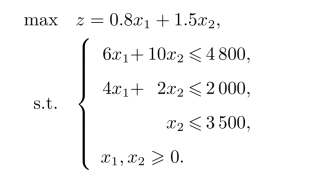
利用LINGO求解后得到最优解：x1=0，x2=480；z∗=720。

把最优解代入约束条件可知，第一个约束条件为紧约束，而第二个、第三个约束条件都为松约束，说明企业资源在一定程度上产生了闲置，而限制企业利润增长的主要原因是由于可用工时有限所造成的。那么企业可以通过加班的方式来增加可用工时，加班应该如何制定呢？根据LINGO最优化的结果知道，工时资源的影子价格为0.15，所以企业只要支付的单位工时费用低于0.15就可选择加班的方式来增加工时量。

另外，还注意到最优方案中是不生产老虎车型汽车的。这对于企业来说也是一种不太现实的安排，如果企业要求老虎车型的产量应不低于狮子车型的产量，最优解会发生什么样的变化呢？企业的这一要求实际上是增加了一个约束x1-x2≥0，将其加入原来的模型中，求解后可以得到：x1=300，x2=300；z∗=690。产量达到了均衡，但企业的利润有所下降。

案例二出版计划

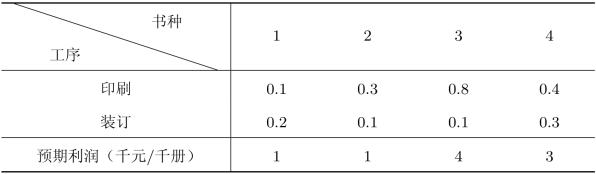
某出版单位有4 500个空闲的印刷工时和4 000个空闲的装订工时，拟用于4种图书的印刷和装订。各种图书每册所需的印刷和装订工时如表2.31所示。

表2.31　案例二的数据

(www.daowen.com)

为了确定最优的图书出版计划，设xj为第j种书的出版数（单位：千册），可以得到如下线性规划模型：

求解得到x1=5，x2=x3=0，x4=10；z∗=35。

(1)若根据市场调查第4种图书最多只能销5 000册，当销量多于5 000册时，超量部分每册降价2元，此时企业的出版计划应作如何调整？

在这种情形下，出版单位首先要考虑第4种图书的出版量是否应该超过5 000册，所以假设超过5 000册的第4种图书为一种新图书5，其出版数量为x5，其预期利润为1，对印刷和装订工时的需求与第4种图书相同，这样可建立一个新的线性规划模型如下：

(2)在不考虑(1)中的情况下，经理对于不出版第2种图书提出意见，要求该种图书必须出2 000册，此时企业的生产计划会怎样变化呢？

这种情况下，由于第2种图书必须出2 000册，可以将出版这2 000册图书的工时耗费去除，即原问题约束条件的右端项分别减少到39和38，再进行求解。也可以直接在原问题增加一个约束条件x2=2进行求解，得到的结果是一致的：x1=7，x2=2，x3=0，x4=8；z∗=33。

(3)作为替代方案，第2种图书仍须出版2 000册，印刷由自己承担，而装订工序外包给其他企业，但装订成本每册高0.5元，求新的最优计划。

这一替代方案影响到原问题中的两个参数：使得系数矩阵中的a22=0，同时c2=0.5。此时得到的新模型为

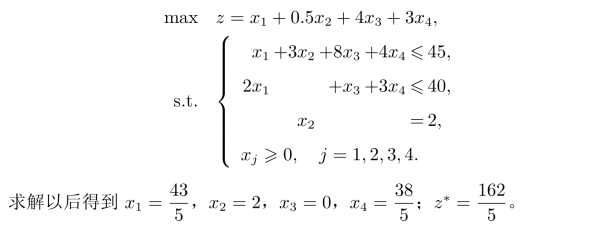
(4)出版第2种图书的另一方案是提高售价，若第2种图书的印刷加装订成本合计为每册6元，则该书售价应为多高时，出版该书才有利。

这个问题实际上是原问题中对于价值系数c2的变化范围的分析，由于其成本为6，所以可以假设x2的价值系数为6+c2，根据最优单纯形表求解σ2≥0得到c2的最小值即可。求解过程此处略去，结果是只有当第2种图书的售价高于8元时，出版该书才是有利的。