由于运输问题是特殊的线性规划问题，且其系数矩阵具有稀疏性，所以通常使用表上作业法进行求解。表上作业法本质上是单纯形法，是对求解运输问题的一种简化方法。下面我们通过实例来说明表上作业法的基本过程。

例2.15(表上作业法)已知某运输问题如表2.20所示。

表2.20　表上作业法的原始数据

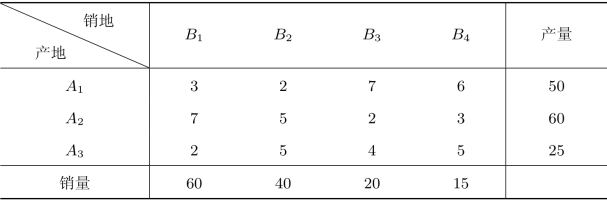
1.初始解的确定

由于运输问题总是存在可行解，所以确定初始解有很多方法。但是一般希望得到初始解的过程既简便，又尽可能地接近最优解。下面介绍两种使用较为普遍的方法：最小元素法和伏格尔（Vogel）法。

(1)最小元素法

最小元素法的基本思想是就近供应，即从单位运价中最小的元素确定调运关系，然后次小，直至得到初始解为止。

首先，在运输问题的表格中找最小元素，为2，而且存在多个。此时任选一个即可，如首先选择c12，即从A1运往B2。A1的产量为50，而B2的需求量为40，所以满足其要求，从A1运送40个单位的物资到B2，之后A1的产量还剩下10，B2的需求量为0，在后续计算中不再考虑B2。如表2.21所示。

表2.21　最小元素法1

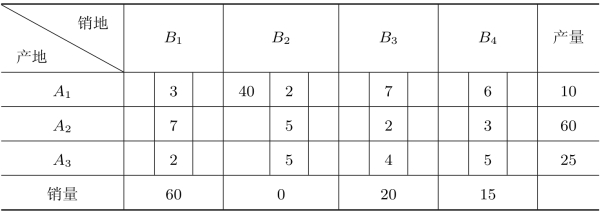
注意表2.21中仍然是一个产销平衡的运输问题，所以重复上一步骤。选择最小元素c23=2，从A2运往B3 20个物资，A2的产量变为40，B3的需求量变为0，后续计算中不再考虑B3。如表2.22所示。

表2.22　最小元素法2

重复上述步骤，最终得到初始方案如表2.23所示。

表2.23　最小元素法

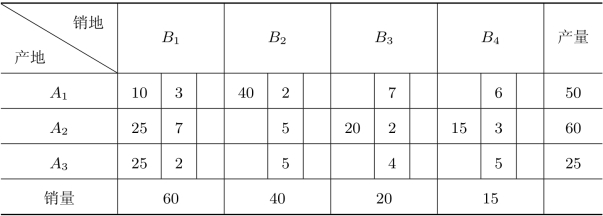
(2)伏格尔法

伏格尔法利用了优化理论中罚函数的思想。由于运输问题的目标函数是最小化的，所以每个产地运出的物资都应该尽量走最小运价的地方，如A1应该尽量运往B2，A2应该尽量运往B3，A3应该尽量运往B1，但是这样做达不到运输问题约束条件的要求。所以，通常还会考虑次小运价，即在走最小运价无法实现要求时，加上次小运价后肯定能够实现运输问题的要求（想想为什么）。但是每一个产地运出的物资应该尽量走最小运价，每一个销地应该尽量从最小运价的地方接货，而且次小运价与最小运价的差额越大，越应该首先考虑。比如，从A1运出的物资，次小运价与最小运价的差额为1，A2的是1，A3的是2，所以从产地的角度来考虑的话，应该首先考虑让A3运出的物资走最小运价，不然走次小运价增加的运费最多。这一分析过程对于销地也是一样的。这就是伏格尔法的基本思想。

具体而言，在使用伏格尔法寻找初始方案时，首先分别计算行差与列差（次小值-最小值），然后由最大差额所在行或列的最小元素所在位置确定调运关系，分配运量之后得到一个新产销平衡的运输问题，再重复这一步骤直至得到初始方案。

如在本例中，首先计算各行各列差额如表2.24所示。

表2.24　伏格尔法1

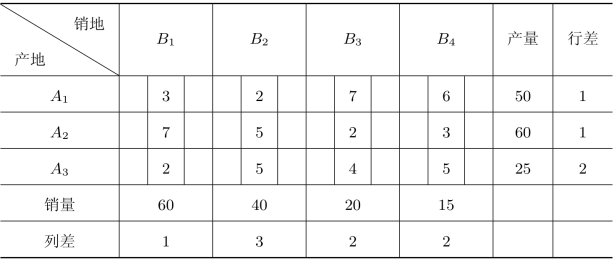
由表2.24可知，B2所在列的差额最大，所以首先应该考虑运往B2的物资应该走最小运价，即应首先考虑从A1运往B2，A1的产量为50，B2的需求量为40，所以分配运量40。如表2.25所示。

然后不再考虑B2，重新计算行差，再确定调运关系，直至得到初始方案，如表2.26所示。

表2.25　伏格尔法2

(www.daowen.com)

表2.26　伏格尔法

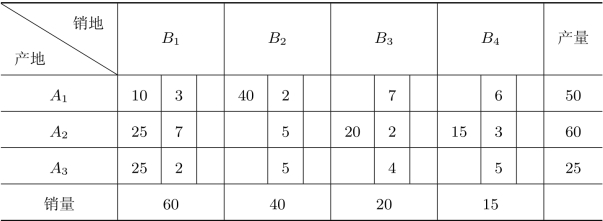
2.最优性检验

最优性检验用于判断前面得到的初始方案是不是总运费最小的最优方案。首先注意到运输问题是目标函数最小化的线性规划问题，所以，如果能够按单纯形法得到其检验数的话，最优性条件应该是所有检验数都不小于0。

计算运输问题检验数最为常用的方法为位势法，它来源于对偶理论。设(u1,u2,···,um,v1,v2,···,vn)是对应于运输问题m+n个约束条件的对偶变量。根据对偶理论可知

另外，运输问题中决策变量xij的系数向量为pij(pij中只有第i个和第m+j个位置为1，其余均为0)，于是，决策变量xij的检验数为

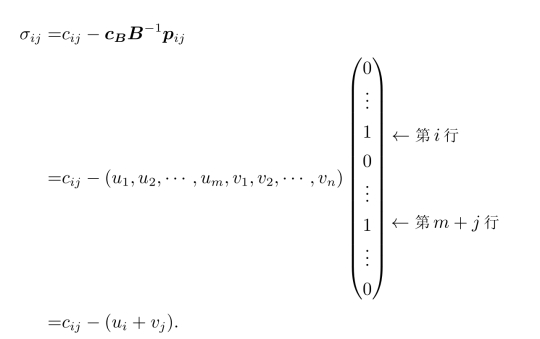
通常可以根据基变量的检验数为0这一要求，求解出所有的ui和vj的值，再根据这些值就可求出非基变量的检验数了。但是在求解ui和vj的值时，只有m+n-1个基变量，即只有m+n-1个关于ui和vj这m+n个变量的方程，这样是无法确定ui和vj的值的。这是因为运输问题只有m+n-1个有效约束条件，本应该对应着m+n-1个对偶变量，说明我们多假设了一个对偶变量，这种情况可以通过令ui和vj中某一个值为0来解决，通常令u1=0。具体计算过程如下（见表2.27）：

表2.27　最优性检验—位势法

首先，根据σB=0求ui和vj的值，即

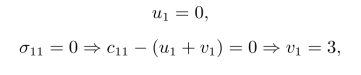
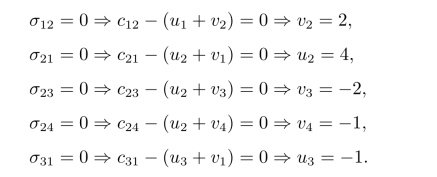
然后，利用σij=cij-(ui+vj)计算所有非基变量的检验数，即

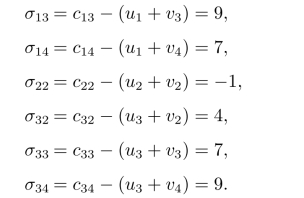
由于σ22=-1<0，说明当前方案不是最优解。

3.方案的调整

根据前面检验数的计算结果，由于σ22=-1<0，所以当前方案不是最优方案，需要进一步调整。根据单纯形法的思路，则x22应该入基成为基变量（方案点），即x22的值应该不为0，说明增加A2到B2的运输量可以减少总的运费。但另一方面，如果x22入基成为了基变量（方案点），那么原来的基变量（方案点）就应该出来一个成为非基变量（非方案点）。那么哪一个应该出基呢？注意到运输问题有产销平衡的要求，如果A2到B2的调运量x22由0变为非0，那么A1到B2的运量就必须要减少，这样A1到B1的运量就要增加，A2到B1的运量就要减少，只有这样才能保证运输问题的约束条件得到满足。

这样的调整过程就形成了一个闭合的回路：x22→x12→x11→x12→x22。在这条闭回路上，奇数点的运量要增加θ，偶数点的运量要减少θ，这样调整后就可得到一个新的运输方案，其中θ=min{xij|xij为偶数点}为调整量，如表2.28所示。

目前，这条闭回路上的调整量为25。调整后的新方案及其检验数计算如表2.29所示。

在调整后的方案中，所有的检验数都不小于0，所以得到的即为最优调整方案，最小费用为z∗=3×35+2×15+5×25+2×20+3×15+2×25=395。

表2.28　方案调整

表2.29　调整后的新方案