技术系数的变化主要是指aij的变化。具体而言，可能包括两种变化：一是新增加（或减少）原来的产品种类；二是原来产品的生产技术发生了变化。

例2.12在例2.1中，企业打算在现有资源条件下，生产一种新产品丙，其市场价格为5，单位产品对三种资源的消耗量分别为1,2,1。试问：企业是否应该生产产品丙？如果生产，其生产计划有何变化？

这样，新产品的检验数为

所以，新产品值得生产。为了得到新的最优解，需要将新产品的相关参数反映到原最优单纯形表中。首先其系数列应为

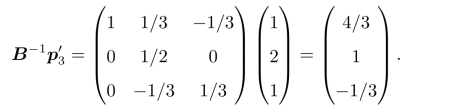
这样考虑到新产品的单纯形表如表2.16所示。

表2.16　灵敏度分析—技术系数的变化一

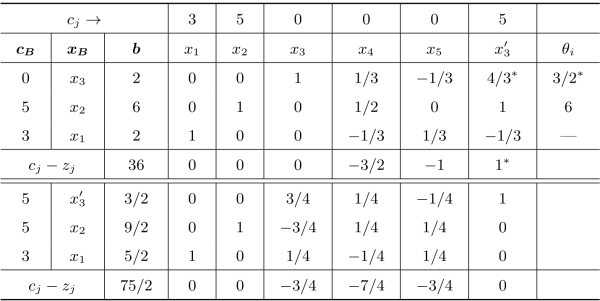
由表2.16可知，新增加一种产品后企业的生产计划变化为甲生产2.5件，乙生产4.5件，丙生产1.5件，企业收益增加到37.5。(www.daowen.com)

下面我们考虑第二种技术系数的变化。

例2.13在例2.1中，假设企业的生产技术发生变化，原来生产产品乙不需要A资源，现假设生产单位产品乙需要1个单位的A，试讨论这种变化对最优生产计划的影响。

解与前例的思路类似，将变化后的乙产品看做一种新产品来考虑。由原最优单纯形表可知，原生产计划中产品乙的产量为6，这样生产技术变化后如果还按原计划生产是无法实现的，因为资源A的供应量只有4，所以这种技术变化会对最优解产生影响。与前例类似，我们将这种变化反映到最优单纯形表中，如表2.17所示。

表2.17　灵敏度分析—技术系数的变化二

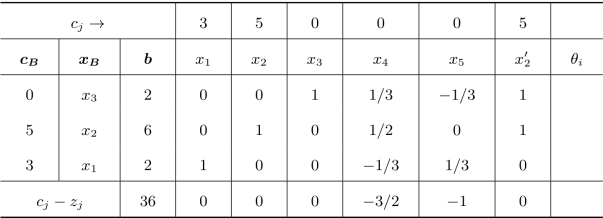
接下来去掉x2列，将x′2列转化为单位列，即用x′2替换x2，然后再根据对偶单纯形进行求解，如表2.18所示。

表2.18　灵敏度分析—技术系数的变化二

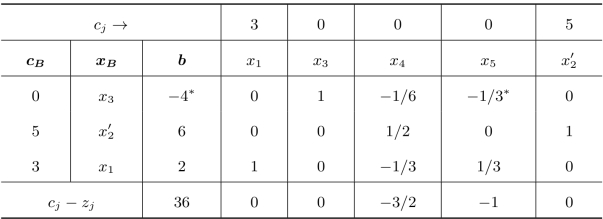
续表

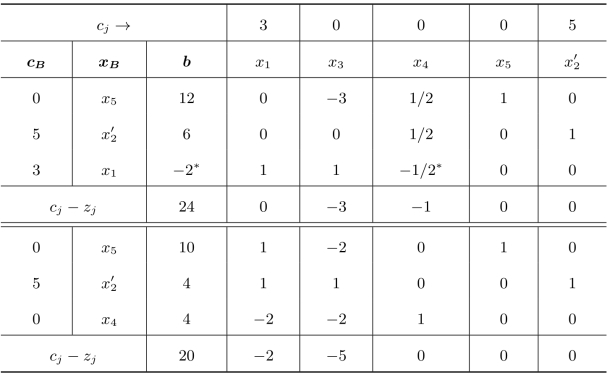
此时得到的最优解为只生产产品乙，其产量为4，企业收益下降到20。