对偶性质的另一个应用就是对偶单纯形法。根据前述性质可知:在单纯形表中进行迭代时,在b列中得到的是原问题的基可行解,而在检验数行得到的是对偶问题的基解。在初始单纯形表中,可以发现原问题得到的是一个基可行解(≥0),而对偶问题的解是一个非可行解(检验数行的相反数有小于0的)。单纯形表的过程就是在保证原问题为基可行解的条件下,逐步通过迭代运算和行变换将对偶问题的解由非可行解转化为可行解(检验数行的相反数都不小于0),此时原问题和对偶问题都为可行解,根据对偶性质,原问题和对偶问题都达到了最优解。
由于原问题与对偶问题是相互对称的,所以也可将上述思路反过来考虑,就形成了对偶单纯形法的思路。即:如果原问题的解是非可行解(b列存在负值),也可以在保证对偶问题的解为基可行解的条件下(检验数行不大于0),逐步通过迭代运算和行变换将原问题的解转化为可行解,当双方都达到基可行解时,原问题和对偶问题也都达到了最优解。
具体而言,对偶单纯形法的计算步骤如下:
(1)根据线性规划问题列出单纯形表。检查b列的值,若都为非负,检验数都为非正,则已得到最优单纯形表,停止计算。若检查b列的值时存在负分量,而检验数均不大于0,则进行下一步。于是确定非基变量xk为换入变量。

(4)以xl为出基变量、xk为入基变量进行迭代运算,得到新的单纯形表。然后,转到步骤(1)。
例2.9(对偶单纯形法)用对偶单纯形法求解下列线性规划问题:
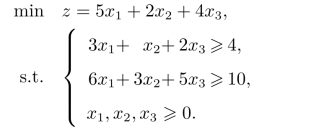 (https://www.daowen.com)
(https://www.daowen.com)
解首先注意到,如果按原问题的单纯形表进行求解,需在两个约束条件中加入剩余变量和人工变量才能得到初始单纯形表。但是,如果应用对偶单纯形法则不用如此麻烦了,可以先在约束条件的两边分别乘-1,然后各自加一个松弛变量即可。即标准化得到
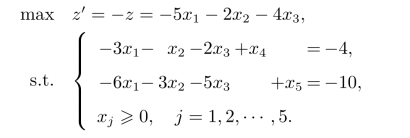
建立此问题的单纯形表,然后利用对偶单纯形法进行求解,具体过程如表2.14所示。
表2.14 对偶单纯形法的求解过程
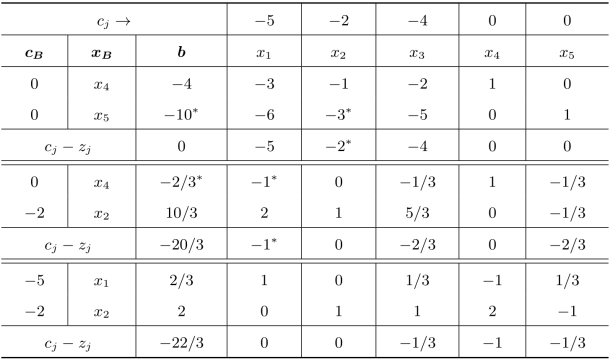
表2.14求解过程最后一步中,所有的检验数均不大于0,而且b列值均不小于0,所以为最优单纯形表。原问题的最优解为
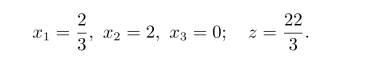
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







