【摘要】:对偶问题的解与原问题检验数的对应关系原问题单纯形表的检验数行对应其对偶问题的一个基解。表2.13中,ys1对应原问题中基变量xB的剩余变量,ys2对应原问题中非基变量xN的剩余变量。这些对偶问题的基本性质有着十分重要的应用,尤其是互补松弛性为我们提供了原问题与对偶问题最优解之间的对应关系。
对偶问题与原问题之间存在着密切的关联性,下面的这些性质更加清楚地说明了这种联系,而且这些性质也为求解与分析线性规划提供了一些便利。
对称性对偶问题的对偶是原问题,或者说对偶问题与原问题是互为对偶关系。

无界性若原问题(对偶问题)为无界解,则其对偶问题(原问题)无可行解。反过来不一定成立,即当原问题(对偶问题)无可行解时,其对偶问题(原问题)或具有无界解或无可行解。

对偶定理若原问题有最优解,那么对偶问题也有最优解,且目标函数值相等。

对偶问题的解与原问题检验数的对应关系原问题单纯形表的检验数行对应其对偶问题的一个基解。其对应关系如表2.13所示。
表2.13中,ys1对应原问题中基变量xB的剩余变量,ys2对应原问题中非基变量xN的剩余变量。另外也可以发现对偶问题的解为y=cBB-1。(www.daowen.com)
这些对偶问题的基本性质有着十分重要的应用,尤其是互补松弛性为我们提供了原问题与对偶问题最优解之间的对应关系。
表2.13 对偶问题的解与原问题检验数的对应关系

例2.8(互补松弛性的应用)已知线性规划问题
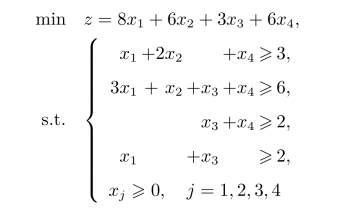
的最优解为x∗=(1,1,2,0)T,试根据对偶理论,直接求出对偶问题的最优解。
解首先写出该问题的对偶问题如下:

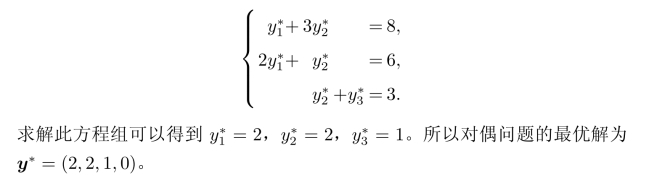
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关管理运筹学方法的文章








