在例2.1中,我们讨论了某企业在三种原材料供应量有限情况下的产品甲、乙的最优组合问题。现在如果企业决定不生产甲、乙两种产品,而将其所拥有的资源A,B,C卖掉,那么企业应该如何来确定每种资源的价格呢?首先,企业如果决定不把资源用来生产产品而将资源出售,则意味着企业出售资源的收益不会低于生产产品所获得的收益。
现假设三种资源的价格分别为y1,y2,y3。如果企业认为出售资源比生产产品更为有利,则意味着将生产产品甲应消耗的资源出售后的收益是不会小于生产产品甲的收益的,即存在
![]()
同理,对于产品乙也会存在
![]()
企业出售资源时的目标函数为
![]()
其中,ω为出售三种资源所获得的总收益。从企业的角度来看当然ω越大越好,但从买方的角度来看他的支付越少越好。而且,在满足(2.15)和(2.16)的情况下(即出售资源比生产更有利的情况下),只有当前目标函数值最小化才具有现实意义,不然资源定价将会是无穷大,那么定价也就没有任何现实意义了。
将上述约束条件和目标函数综合起来,得到了一个新的线性规划模型,称之为原问题的对偶问题。为了进行对比,我们将原问题和对偶问题都列在了下面:
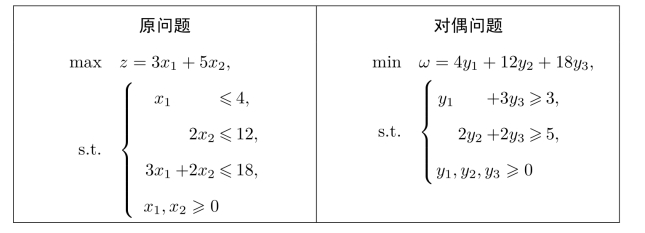
对照这两个线性规划问题,可以发现:
(1)原问题的目标函数是最大化的,而对偶问题的目标函数是最小化的。
(2)原问题的价值系数成为对偶问题的资源向量,而原问题的资源向量成为了对偶问题的价值系数。(www.daowen.com)
(3)原问题共有3个约束条件,对应着对偶问题有3个变量;而原问题有2个变量,对应着对偶问题有2个约束条件。
(4)原问题的约束条件都是≤型的,对应着对偶变量都是非负的;而原问题的变量都是非负的,对应着对偶问题的约束条件都是≥型的。
将上述规律一般化后可以得到更一般情况下原问题与对偶问题之间的关系:

这里y=(y1,y2,···,ym)。
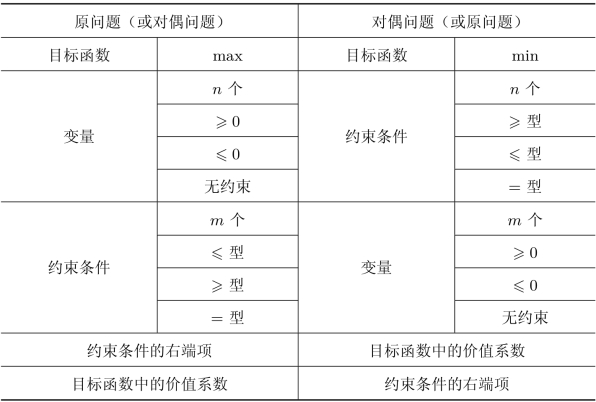
在更一般情况下,线性规划问题不一定满足上述形式的要求,所以我们将更一般情况下原问题与对偶问题之间的关系列于表2.12中。
表2.12 原问题与对偶问题的对应关系
例2.7写出下列线性规划问题的对偶问题:
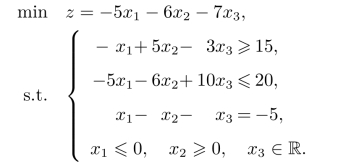
解假设该问题的对偶变量分别为y1,y2,y3,根据原问题与对偶问题的关系,得到该问题的对偶问题为
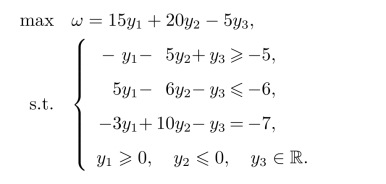
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






