前面提到线性规划问题也可以用矩阵形式进行表达，下面将结合单纯形法的步骤来说明线性规划问题求解过程中相关参数的矩阵描述方式，这将有助于加深对单纯形法的理解，以及为对偶理论和灵敏度分析打下基础。

设有线性规划问题

使用单纯形法求解，给该线性规划问题约束条件加上松弛变量xs=(xn+1,xn+2,···,xn+m)T，使线性规划问题化为标准形式：

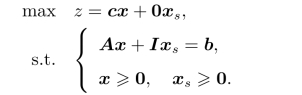
选取松弛变量xs为基变量，此时基解xs=b，目标函数值z=0，非基变量的系数矩阵为A，非基变量的检验数为c。一般情况下，假设该线性规划问题的一个可行基为B，则可将上述标准形的决策变量分为(xB,xN,xs)T，其中xB为基变量，它的分量分别为B矩阵的列向量所对应的变量；xN和xs为非基变量，xN由基变量和松弛变量以外的其他变量所构成。同样可将系数矩阵A划分为(B,N)，价值系数向量c划分为(cB,cN)，这样上述标准形就可写成

为了得到基变量xB的值，将第一个约束条件移项并两边左乘B-1，得

将上式代入问题的目标函数得

令非基变量xN=0，xs=0，得到问题的一个基可行解：

对应的目标函数值为

(www.daowen.com)

从上述单纯形法的基本过程中可以得到，若xB为线性规划问题的一个基可行解，则有

(1)线性规划问题的基变量的值为

(2)线性规划问题的目标函数值为

(3)线性规划问题的检验数为

这是因为，从(2.14)可以看到非基变量xN的系数为cN-cBB-1N，即为非基变量xN的检验数，而基变量xB的检验数为零，且存在cB-cBB-1B=0，所以σ包含了xB和xN的检验数；σs是松弛变量xs的检验数；

(4)线性规划问题的θ规则可以表示为

这里pj是变量xj的系数向量;

(5)根据上述过程也可以得到单纯形表的矩阵描述如表2.11所示。

表2.11　单纯形表的矩阵描述