上述单纯形法的求解过程是基于标准形的线性规划问题展开的，而实际问题中并不一定能够满足标准形的要求；此外，在使用单纯形法求解时可能会产生退化问题。因此，本节针对单纯形法中可能出现的问题作进一步讨论。

1.不同的检验数形式

上面所述单纯形法是以标准形的线性规划问题为基础的，其最优性检验的标准为cj-zj≤0。但在实际应用中还会存在其他形式的检验数，它们本质上是一致的，为了避免混淆，现将几种情况作一归纳，见表2.7。

表2.7　检验数的不同形式

2.初始基的构造

在使用单纯形法求解线性规划问题时，第一步是以松弛变量为基变量得到的初始基，这是因为加入的松弛变量正好构成了一个单位矩阵，这样做有两个好处：一是不用人为地确定基变量，然后将其系数矩阵转化为单位矩阵；二是以单位矩阵开始运算，计算相对简单。但当约束条件不是≤型时，加入的松弛变量就不一定能构成一个单位矩阵，此时就需要人为地加入一些人工变量，使得初始单纯形表包含一个单位矩阵。这种方法称为人工造基方法，常用的人工造基方法有两种，即大M法和两阶段法。下面通过一个实例来说明这两种方法的求解过程。

例2.5(大M法)试用单纯形法求解如下线性规划问题：

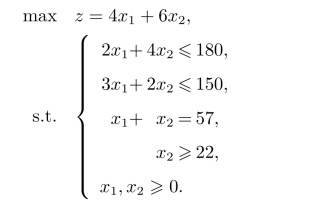
解首先对该问题进行标准化处理，得到

上述标准化模型中，系数矩阵中并不存在单位矩阵，无法确定初始可行基。因此，我们在第三、第四个约束条件中人为地加上人工变量，使其包含单位矩阵。但是，加入人工变量后还要保证与原模型一致，而要实现这一点只有当人工变量的值为0时才行，所以我们让人工变量在目标函数中的系数为-M，其中M为任意大的正数。这样，只要原问题有最优解，最后所有的人工变量都将成为非基变量，其值为0，对原问题不产生影响。考虑如下线性规划模型：

利用单纯形表求解，过程如表2.8所示。

表2.8　大M法的单纯形表

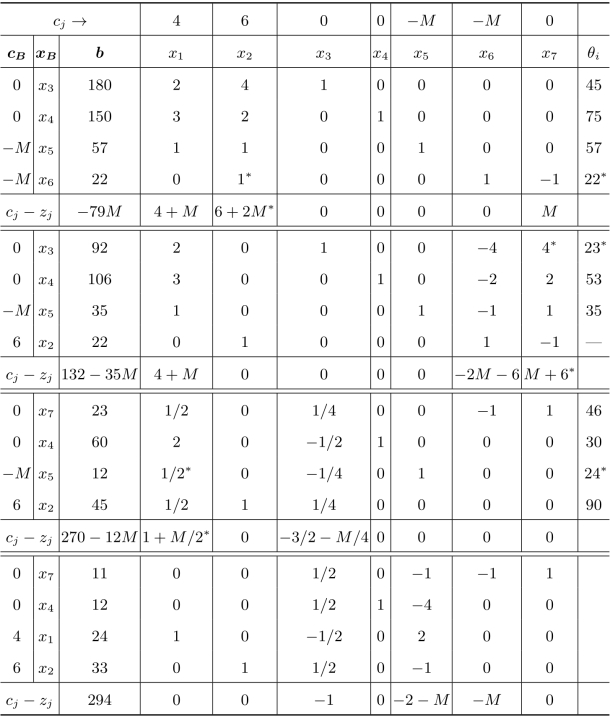
检验数均不大于0，单纯形表已达到最优。而人工变量不在基变量中，所以原问题存在最优解为

两阶段法第一阶段不考虑原问题是否存在基可行解，给原线性规划问题加入人工变量，并构造仅含人工变量的目标函数且要求实现最小化，如

(www.daowen.com)

然后用单纯形法求解上述模型，若得到ω=0，则说明原问题存在基可行解，可进行第二阶段计算；否则原问题无可行解，应停止计算。第二阶段：在第一阶段计算得到的最终表中除去人工变量，将目标函数行的系数换回原问题的目标函数系数，作为第二阶段计算的初始表。

例2.6(两阶段法)利用两阶段法求解例2.5。

解首先，第一阶段的模型为

利用单纯形表求解，如表2.9所示。

表2.9　两阶段法—第一阶段

续表

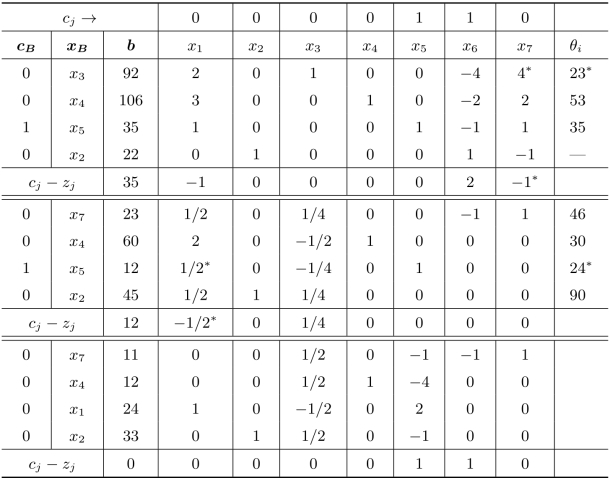
第一阶段求得ω=0，人工变量x5=x6=0。说明原问题存在最优解，而且现在的单纯形表中已经得到由原问题的变量所构成的一个单位矩阵，所以可以进行第二阶段的计算。将第一阶段的最终表中人工变量取消并填入原问题的目标函数的系数，进行第二阶段的计算，如表2.10所示。

表2.10　两阶段法—第二阶段

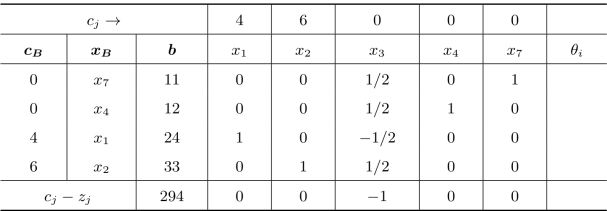
表2.10中，检验数都不大于0，得到原问题的最优解：x1=24，x2=33；z∗=294。

3.退化问题

如果线性规划问题的解中出现了基变量为0的现象，则说明线性规划问题出现了退化。我们知道，单纯形法计算中用θ规则确定出基变量，而有时会存在两个以上相同的最小比值，这样在下一次迭代中就有一个或几个基变量等于零，这就出现了退化解。当出现退化时，线性规划问题可能出现循环，达不到最优解。

尽管计算过程的循环现象很少出现，但还是有可能的。为此，先后有人提出了“摄动法”、“字典序法”等解决这一问题。1974年Bland提出了如下一种简便规则（常称为Bland规则）：

(1)选取cj-zj>0中下标最小的非基变量xk入基；

(2)当按θ规则计算存在两个或两个以上最小比值时，选取下标最小的基变量为出基变量。

可以证明，按Bland规则计算时，一定能够避免出现循环。