仔细回想一下前面的求解过程，可以发现用单纯形法求解线性规划问题的过程主要依赖的是线性方程组的高斯消元法。而这一过程可通过矩阵（或表格）的形式来实现，实现的结果就是单纯形表。一般地，线性规划问题的单纯形表如表2.2所示。

表2.2　线性规划问题的单纯形表形式

表2.2中，xB列中填入基变量，这里是x1,x2,···,xm；cB列中填入基变量的价值系数，这里是c1,c2,···,cm，它们是与基变量相对应的；b列中填入约束方程组右端的常数；cj行中填入变量的价值系数c1,c2,···,cn；θi列的数字是在确定换入变量后，按θ规则计算后的数值；最后一行b列所在位置为目标函数值，各变量对应位置为xj的检验数，所以通常把最后一行也称为检验数行。

仍然以例2.1为例，结合其模型的标准形式(2.10)，将相关参数反映到如表2.3所示的表格中，即得到该问题的单纯形表。

表2.3　初始单纯形表

在表2.3中，第一行表示的是决策变量的价值系数cj，第二行的前面3个单元格分别是基变量的价值系数、基变量、资源向量，后面是所有的决策变量，最右边的θi是用于判断出基变量的参数。表格的中间部分反映的是模型的约束条件，这个问题中有3个约束条件，分别对应着表格的3行。表格的最下面一行为检验数行，是需要计算的，用于判别问题是否达到了最优解，是决定哪一个变量入基的依据。

单纯形法中涉及需要计算的参数包括决策变量的检验数σj、θi值和目标函数值z。由于其推导过程较繁琐，而且也就是上一节内容的数学化，所以此处不作推导，直接给出相关参数的计算公式。

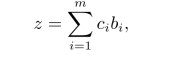
目标函数值的计算目标函数值为其中，ci为基变量的价值系数，bi为基变量的值。它是放在单纯形表最下面一行中的第一个数值，目前z=0。

检验数的计算决策变量xj的检验数为

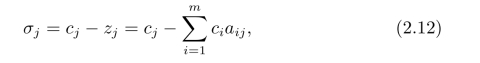
其中，cj为变量xj的价值系数，aij为变量xj的技术系数。检验数处于单纯形表的最下面一行，如当前σ1=3，σ2=5，σ3=σ4=σ5=0。

检验数用于判断单纯形表是否达到最优，在初始单纯形表中，由于非基变量x1和x2的检验数都大于0，说明目标函数值还可增大，所以当前解不是最优解。利用检验数判断解的状态有如下规则：

检验数的第二个作用是判断哪一个非基变量入基，一般地，我们选择正的检验数中最大检验数对应的变量入基，可以使目标函数增加更快，即若

则xj∗入基。

θi值的计算若已决定xj∗为入基变量，则(www.daowen.com)

其中为基变量当前值，aij∗为入基变量当前的技术系数。由上一节所述过程可知，在确定出基变量时，应选择最小θi值对应的基变量出基，即若

则xi∗出基。

单纯形表的完整计算过程如表2.4所示。

表2.4　单纯形表的计算过程

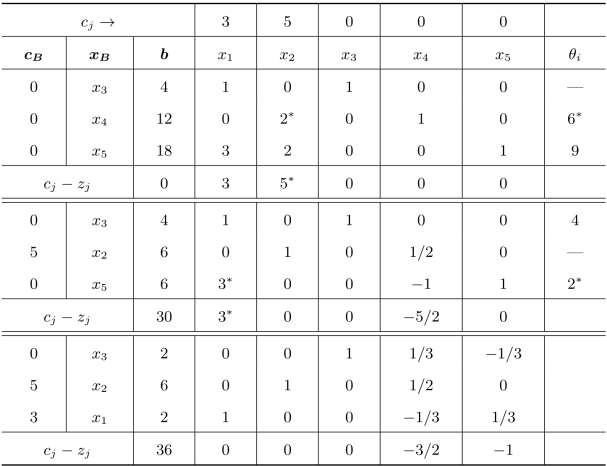
上述单纯形表中最后一行，所有非基变量的检验数都小于0，所以线性规划问题得到了最优值：x∗=(2,6,2,0,0)T，z∗=36。

例2.4利用单纯形法求解下列线性规划问题：

解令y1=x1-1，y2=x2-2，y3=x3-3，则原线性规划问题转化为

标准化后得到如表2.5所示单纯形表求解过程，其中y4,y5,y6为松弛变量。

表2.5　单纯形表

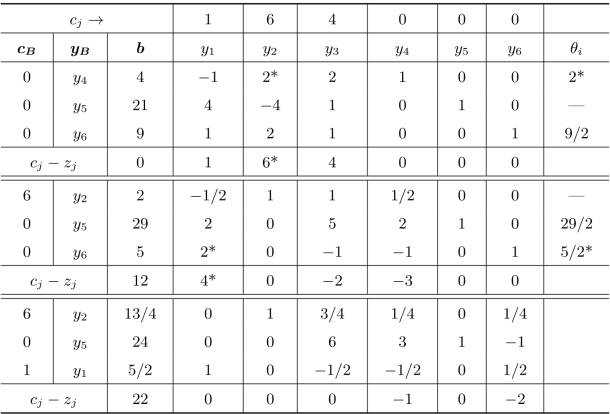
由于所有检验数均不大于0，所以得到问题的最优解。但是注意到非基变量y3的检验数为0，说明问题有无穷多最优解。为了得到另一个最优解，可以让y3入基，如表2.6所示。

表2.6　问题的另一个最优解