下面以线性规划问题的标准形式来说明单纯形法的基本思路。单纯形法本质上是基于几何原理，这也是为什么这个方法叫单纯形法，因为单纯形本身就是一个几何概念。^[1]

根据线性规划问题的标准形式可以发现其约束条件（除非负约束外）构成一个线性方程组，如果这个方程组具有唯一解，则可容易地得到线性规划问题的解。但由于该方程组系数矩阵A通常情况下不是一个满秩矩阵，所以不能得到一个确定解，而是得到了无穷多解（如果可行域存在），这些解构成了该线性规划问题的可行域。而我们知道，线性规划问题的可行域如果存在，应为一凸集，所以可以通过该凸集的顶点坐标的凸组合方式来描述它，即将其表示为一个单纯形。而且我们还知道，线性规划问题的最优解不可能在可行域的内部实现，这样首先需要知道可行域的顶点如何得到。

假设有办法确定可行域的顶点，接下来要判断的是哪一个顶点可以使得目标函数实现最大化。显然不能把每个顶点都代到目标函数中来实现这样的判断。一种科学的方法是：首先确定一个可行解，得到了目标函数值，再判断该点是不是最优解；如果是，则求解结束；如果不是，那么就需要设计一种机制去寻找下一个可行解，而且要保证新得到的可行解比上一个更优；一直重复这个过程，就可得到线性规划问题的最优解。

所以，单纯形法的关键在于解决以下3个问题：

(1)如何简单方便地确定一个初始可行解？

(2)如何判断可行解的最优性？

(3)如何实现从一个可行解转换到下一个可行解，而能够使目标函数值更优？

下面将结合例2.1来说明单纯形法的基本思路，即如何解决上述3个基本问题。需要说明的是，这个过程会使用到线性规划的基本性质与定理，如果有兴趣的话，可以参考相关的文献。

首先将例2.1的线性规划模型转化为标准形式，可以得到

根据前述思路，我们需要以约束条件构成的方程组为基础，寻找一个初始可行解。根据线性代数的知识可知，利用高斯消元法可以求解线性方程组，将变量的系数矩阵通过行初等变换变化为单位矩阵即可求解。这里借鉴这种思路，注意到在该线性规划问题的约束条件构成的方程组中，变量x3,x4,x5对应的系数矩阵为一个单位矩阵，所以可以这3个变量为方程的未知变量，而把x1和x2作为参数，求解此方程组，即可得到

将它们代入目标函数，可以得到此时

由于当前解中x3,x4,x5是以x1,x2为参数的，所以存在着无穷多解。而前面说过，只需确定可行域的顶点。为了达到这一目的，令x1=x2=0，可以得到该线性规划问题的一个解x(0)=(0,0,4,12,18)T，此时z=0。注意x(0)是一个可行解，至此我们回答了上面提出的第一个问题。

通常我们把x3,x4,x5称为基变量，把基变量的系数构成的矩阵称为基。把基变量之外的变量称为非基变量，如此时的x1和x2。可见，基是指系数矩阵中取出来的一个非奇异方阵B。当令所有的非基变量等于0时，可以得到一个解，这个解称为基解，如果它还满足非负的要求，则称它为基可行解。这里所得到的就是一个基可行解，事实上按照上述步骤，只要存在b≥0就可保证得到的初始解为基可行解。

另外，有定理保证基可行解对应于可行域的顶点，如现在的解对应着可行域的顶点(0,0)。这样只需要找到问题的所有基可行解就可以确定目标函数的最优值了。

接下来要判断当前解是不是最优解。根据当前目标函数的表达式(2.11)，为了得到初始基可行解，前面人为地让非基变量x1和x2为0，所以当前目标函数的值为0。但是，目前x1和x2在目标函数值中的系数都是大于0的，这说明只要增加x1和x2的值，目标函数的值就会增加。由此可见，当前解并不是最优解。这就解决了前面提出的第二个问题。

既然当前解不是最优解，那么就需要构造另一个基可行解。在构造新可行基的过程中有两个基本要求：一是目标函数值要增大，而且增大得越快越好；二是要保证新得到的基仍然是可行的。首先，由前面分析可知，无论x1或x2不为0，目标函数值都能增大，但是注意到x2的系数是5，大于x1的系数，所以增加x2的值会使z增大得更快。按照前面的思路与过程，x2的值要不为0，它就必须成为基变量，所以x2要入基，成为基变量。另一方面，基是一个非奇异方阵，如果x2入基成为基变量，势必就要换出一个原来的基变量。无论哪一个变量出基，都要保证基的可行性，即(www.daowen.com)

由此可见，要保证新基的可行性，上述约束条件必须成立，即第二个约束条件限制了x2增长。或者要使得x2的值增加最多，就必须让x4为0，即x4要出基成为非基变量。这样以x2替代x4后得到

整理后得到

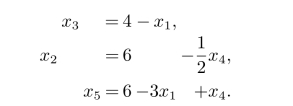
此时，目标函数为

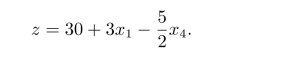
与前类似，令所有非基变量为0，可得x(1)=(0,6,4,0,6)T，z=30。注意x(1)仍是基可行解，而且目标函数由0增加到了30。这样就解决了前面提出的第三个问题。

重复前面的步骤，此时目标函数中x1的系数为3，增加x1还会使目标函数值增大，所以让x1入基。而另一方面，还有

所以，x5出基。可以得到

此时目标函数为

令非基变量x4=x5=0得到x(2)=(2,6,2,0,0)T，z=36。此时，由于目标函数非基变量的系数均小于0，增加它们的值只会使目标函数值减小，所以得到的解x(2)即为线性规划问题的最优解。

通过此例可以将单纯形法的基本过程总结如图2-3所示。

图2-3　单纯形法的基本过程