在企业的生产经营与管理活动中经常会遇到如何合理有效利用有限的资源（如人力、物力、财力等）以达到最好的经济效果的问题。

例2.1(产品组合问题)某企业在某一计划期内要安排生产甲、乙两种产品，已知生产单位产品需要三种原材料A,B,C。两种产品的单位利润、三种原材料的供应量以及生产单位产品的资源消耗如表2.1所示。

表2.1　产品组合问题的相关数据

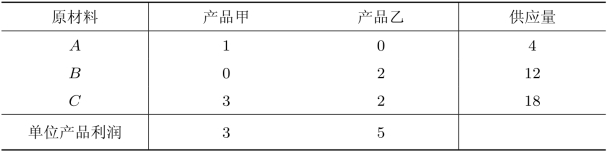
问：企业应该如何制定该计划期内的生产计划，才能使得企业的利润达到最大？

这是一个十分普遍的问题，即企业在既定资源条件下该如何组织生产，才能获取最大利润。为了求解这一问题，需要建立该问题的数学模型。

假设该计划期内企业生产甲、乙两种产品的产量分别为x1和x2，这样一旦确定了x1和x2的值就相应地确定了企业的一个生产计划。当企业的生产计划为(x1,x2)T时，可以得到企业的利润为

由于企业生产过程中需要耗费一定的资源，而且这种资源一般还存在一个限额。如该问题中，企业生产过程中需要原材料A，而其供应量只有4，所以我们可以得到

类似地，对于B,C两种资源分别存在

(www.daowen.com)

和

此外，由于x1和x2分别表示甲、乙两种产品的产量，所以还存在

因此，该企业在既定计划期的利润最大化问题就是要在满足条件(2.2),(2.3),(2.4)和(2.5)的前提下合理确定x1和x2的值以使得(2.1)的值最大，用数学模型表示就是

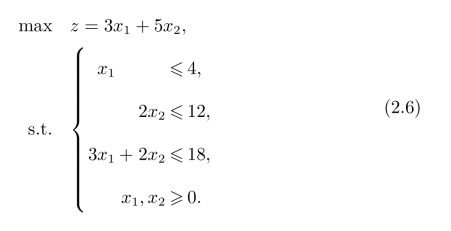
例2.2(人员安排问题)某市一条昼夜服务的公交线路每天各时间区段内所需司机和乘务人员总数如下：

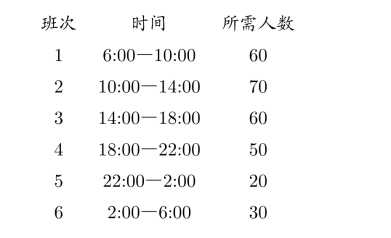
如果司机和乘务人员分别在各时段一开始时上班，并连续工作8小时，问：该公交线路至少应配备多少名司机和乘务人员？

解假设第j(j=1,2,···,6)时段来上班的人数为xj。根据题意要求，可以得到如下模型：

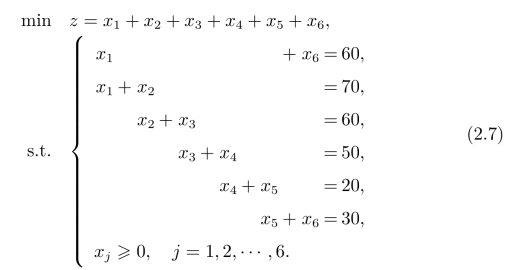
注意到，这里须确定最少需要配备的人数，所以各时段新上班的人数之和应该最小。另外，每时段上班的人数不能超过所需人数，不然会不经济，所以上述模型中所有的约束条件都采用了等式。