1.回归分析是通过一个变量或一些变量的变化解释另一变量的变化，用适当的数学模型去近似地表达或估计变量之间的平均变化关系。

2.回归分析的种类：按自变量的个数分，有一元回归和多元回归；按回归曲线的形态分，有线性（直线）回归和非线性（曲线）回归。

3.回归分析的主要步骤：第一步，根据理论和对问题的分析判断，将变量分为自变量和因变量。第二步，设法找出合适的数学方程式（即回归模型）描述变量间的关系。第三步，对回归模型进行统计检验。第四步，利用回归模型，根据自变量去估计、预测因变量。

4.直线方程只有一个因变量和一个自变量，且变量的次数只有一次，称为一元线性回归方程。运用一元线性回归方程来分析因变量对自变量的依存关系就是一元线性回归分析。在相关图中，如果自变量与因变量对应的散点图近似为直线，或计算出的相关系数具有显著的直线相关关系，就找一个“直线方程y=kx+b”来具体表示这种直线相关关系。

用最小二乘法来求直线方程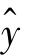=kx+b中的斜率k和截距b。

5.回归系数与相关系数有着非常密切的数量关系，相关分析与回归分析两者可互相推算。

6.回归方程的计算值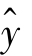 与实际值y 存在差距，这差距用估计标准误差（Sy）来表示。估计标准误差Sy是衡量回归直线代表性大小的统计分析指标，它说明观察值围绕着回归直线的变化程度或分散程度。

7.估计标准误差与相关系数的关系：Sy=σy。

8.总离差平方和（SST）=剩余平方和（SSE）+回归平方和（SSR）

9.把回归平方和与总离差平方和之比定义为样本判定系数，记作r2，是回归直线与样本观测值拟合优度判定的指标。r2的值为0～1，r2越大，拟合优度就越好；如r2不大，说明模型中给出的x对y的信息还不够充分，应进行修改，使x对y的信息得到充分利用。

10.多元线性回归分析是研究两个或两个以上的自变量对一个因变量数值的影响。多元回归方程的建立：设因变量y受x1，x2，x3，…，xm等m个自变量的影响，则因变量y 倚各个自变量xj的多元线性回归方程的基本形式为

式中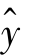：是y的回归估计值，B1，B2，B3，…，Bm是对应于各个变量xj的回归系数，B0是常数项。求解多元线性回归方程的常用方法仍然是最小平方法。按最小平方法的基本要求，通过对每个回归系数求偏导数，并令其等于0，便可得下列m+1 个正规方程组成的方程组

根据资料，计算各个有关数据后，可代入方程求解出各个回归参数的值。

11.多元线性回归模型的检验

（1）拟合程度的评价

在多元线性回归分析中，总平方和的分解公式依然成立。为了判断一般线性模型（非一元线性模型）与数据的拟合程度，需要计算一个多重判定系数R2。

（2）多元线性回归的回归标准差

sy=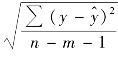，n 为样本容量，m 为回归系数个数。

（3）回归方程的显著性检验（F检验）(www.daowen.com)

F检验是检验自变量与因变量总体的线性关系（对线性模型而言），检验整体参数的显著性。

假设：H0：B1=B2=…=Bm=0，H1：Bj（j=1，2，…，m）不全为零。

构造统计量：F=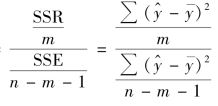～F（m，n-m-1）

给定显著性水平α，计算临界值Fα（m，n-m-1）

F≤Fα（m，n-m-1），接受零假设，说明B1=B2=…=Bm=0，方程中所有自变量联合起来对因变量的影响不显著；F>Fα（m，n-m-1）拒绝零假设，说明Bj（j=1，2，…，m）不全为零，方程中所有自变量联合起来对因变量有显著影响。

（4）回归参数的显著性检验（t检验）

通过F检验，说明整体参数中至少有一个是显著的，但不一定都是显著的。t检验是检验单个参数的显著性，通过t检验说明被检验的参数是显著有效的，如果不能通过t检验的话，说明该自变量对因变量的解释作用不大，应该在模型中剔除。

假设：H0：Bj=0，H1：Bj≠0

构造统计量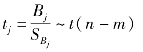

其中SBj是第j 个参数估计值的标准差，sbj=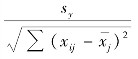

给定显著性水平α，计算临界值（n-m-1）

（n-m-1）接受原假设，说明其他自变量不变的情况下，自变量xj对因变量y没有显著影响。，拒绝原假设，说明其他自变量不变的情况下，自变量xj对因变量y影响显著。

12.可线性化的曲线回归

（1）可线性化的常用曲线类型（表1）

表1　常见的可化为线性的曲线方程

（2）在非线性回归分析中，可用非线性判定系数R2来度量两变量之间非线性相关的密切程度。R2的变化范围介于0 与1，R2越接近于1，表明变量间的非线性相关的程度越强，所配合的曲线效果越好，反之，R2越接近于0，表明变量间非线性相关程度越弱，所配合的曲线效果越差。

13.利用SPSS 进行回归分析的应用。

14.在回归分析中，寻找的是变量间的关系，代表这种关系的函数就是所期望的结果，也可能是所期望的均值。在相关分析中需要度量的是两个或两个以上随机变量之间线性关系的强度。当二维数据显示在散点图上落在一条直线附近时，它们支持一个线性关系，但是这并不能证明这是必然的和有因果的。