1.研究社会现象与现象之间有无关系、相关的密切程度、相关的形式等，称为相关分析。

2.现象间的依存关系大致可以分为函数关系和相关关系。函数关系，即现象之间存在严格的确定性的依存关系，表现出一现象取某一个值时另一现象有确定的值与之相对应，这种对应关系，可以用数学表达式表示。相关关系，即客观现象之间存在的、数量上不一一对应的依存关系，表现出一现象变化另一现象也随之变化，一现象变化取某一个数值时另一现象变化可能有若干数值与之相对应。

3.相关关系类型：按涉及变量的多少分为单相关、复相关和偏相关；按相关形式分为线性相关和非线性相关；按相关方向分为正相关和负相关；按相关程度分为完全相关、完全不相关和不完全相关。相关分析按所依据的变量性质分为可控相关分析和不可控相关分析。

4.相关表：直接根据现象之间的两个变量的原始资料所列出的一一对应而平行排列的统计表。观察相关表中两变量的依存关系，从一变量由小到大的顺序排列看配对的另一变量的变化趋势，若是降低的趋势，则两变量是负相关，反之，则是正相关。若变化比较均匀，则两变量是直线相关，反之，则是非线性相关。

5.相关图：将相关表中一一对应的有序实数用坐标平面内的点来表示，用以表明相关点分布状况的图形，它又称散点图。把坐标平面内的点用线依次连接起来，观察其形状：如果连线呈直线型，两变量就是直线相关；如果连线呈曲线型，两变量就是曲线相关；如果连线由左向右上角倾斜，两变量就是正相关；如果连线由左向右下角倾斜，两变量就是负相关。

6.相关系数是用以反映变量之间相关关系密切程度的统计指标。

r=，σx为x 变量的标准差；σx为y 变量的标准差；cov（x，y）为两个变量的协方差。

（1）取值范围：

（2）当≤1 时，x 与y 之间存在确定的函数关系。

（3）当0 <r<1 时，x 与y 呈正相关；当-1 <r <0 时，x 与y 呈负相关。当r =0 时，x 与y不相关。

（4）当0 <<1 时，表示两变量存在一定程度的线性相关：越接近1，两变量间线性关系越密切；越接近于0，表示两变量的线性相关越弱。(www.daowen.com)

（5）当<0.4 时，x 与y 为低度线性相关；当0.4≤<0.7 时，x 与y 为显著性相关；当0.7≤<1 时，x 与y 为高度线性相关。

7.复相关是反映一个要素或变量同时与几个要素或变量之间的相关关系。复相关系数用R 表示，复相关系数越大，表明要素或变量之间的线性相关程度越密切。

R=，式中为多元线性趋势值或回归估计值。

8.偏相关分析是指当两个变量同时与第三个变量相关时，将第三个变量的影响剔除，只分析另外两个变量之间相关程度的过程。

变量x1，x2之间除去x3的影响后的相关系数，记为r12，3，称为x1，x2对x3的偏相关系数。

r12，3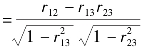，r12表示x1与x2之间的相关系数，r13表示x1与x3之间的相关关系，r23表示x2与x3之间的相关系数。

一般地，偏相关系数计算公式

9.在时间序列中，后期的数值与前期的数值表现出相关关系，称为时间序列自相关。时间数列的自相关也分为线性相关和非线性相关、正相关和负相关等不同种类。

10.相关分析的Excel 及SPSS 操作及结果解读。