1.参数估计就是用样本统计量来估计总体未知参数的方法。

2.点估计也称定值估计，它是用抽样得到的样本指标数值直接作为总体参数估计值的一种推断方法。

3.同一个总体参数可用多个样本统计量来估计，衡量估计量的优良性有无偏性、有效性、一致性三种标准。

4.点估计有矩估计法、顺序统计量法、最大似然法、最小二乘法等。

5.区间估计是利用样本资料计算的统计量来估计总体参数所在的范围，并给出一定的概率保证。总体参数所在的范围称为置信区间，概率保证称为置信度。置信度1-α 越大，估计的可靠程度越高，总体参数真值落入置信区间的可能性越大。但当样本容量一定时，置信度的增加必然带来置信区间的增大，从而降低估计的精确度。

6.一个总体参数的区间估计有总体均值、总体比例和总体方差。估计的条件不同，如总体分布是否已知、总体方差是否已知或相等、大样本还是小样本决定了总体参数区间估计表达式的不同

（1）正态总体且总体方差σ2已知，求μ 的置信区间。

总体均值μ 的1-α 的置信区间为：

μ∈为样本均值，是抽样平均误差ux，是概率度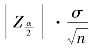，是抽样允许误差。

（2）正态总体且总体方差σ2未知，求μ 的置信区间。

总体均值μ 的1-α 置信区间为

（3）非正态总体，求μ 的置信区间。

当样本容量足够大（n≥30）时，样本均值x 的抽样分布逼近于正态分布。

总体均值μ 的置信度为1-α 的置信区间为

7.总体成数的置信区间

当n 足够大（np >5，n（1- p）>5）时，样本成数p 近似服从正态分布，总体比率π 在（1-α）置信水平下的置信区间为：(www.daowen.com)

8.正态总体方差的置信区间

总体方差σ2的置信度为1-α 的置信区间为

9.两个总体参数的比较，即比较两个总体的均值、两个总体的比例和两个总体的方差是否存在显著差异，一般可以通过两个总体均值之差、两个总体比例之差、两个总体方差之比的区间估计来进行比较。

10.两个总体均值之差的置信区间

（1）两个正态总体且总体方差已知

μ1-μ2的置信度为1-α 的置信区间为

（2）两个正态总体且方差未知但相等

μ2-μ2的置信度为1-α 的置信区间为

（3）两个非正态总体，求两个总体均值之差的置信区间

设两总体X1和X2是非正态分布，且方差未知，当n1和n2足够大时，μ1-μ2的置信度为1-α的置信区间为

11.两个总体成数之差的置信区间

样本容量足够大（n1≥30，n2≥30）时，

π1-π2的置信度为1-α 的置信区间为

12.两个正态总体方差之比的置信区间