1.变异指标又称标志变异指标，是用来说明总体各单位标志值变异程度和离散趋势的指标。它反映分配数列中以平均数为中心各标志值的变动大小范围或差异程度，是说明总体分布特征的一个重要综合指标。

2.变异指标的作用：①变异指标可以测定平均指标的代表性高低程度。总体的变异指标越大，平均指标的代表性越差；反之，变异指标越小，平均指标的代表性越好。②变异指标可以测定数量现象的均衡性、稳定性、整齐性，为有效地组织生产、提高经济管理工作的质量提供依据。

3.全距是总体各单位标志中最大标志值（Xmax）与最小标志值（Xmin）之差。若将研究总体中各个单位，按某一数量标志值的大小顺序排列起来，则最大值与最小值分别处于数列的两极，所以全距也称极差。它表明标志值的变动幅度或范围，通常用R表示，R=Xmax-Xmin。

4.全距的优点在于计算简便，也易于理解。它是粗略地测定变异度的简单方法。但全距这个指标很粗略，它只考虑数列两端数值差异，而不管中间数值的差异情况，也不受次数分配的影响，因而不能全面反映总体各单位标志的变异程度。

5.平均差是总体各单位标志值与其算术平均数的离差的绝对值的算术平均数，反映各标志值与算术平均数之间的平均差异，通常用A.D.表示。平均差越大，表明标志变异程度越大；反之，平均差越小，表明其变动程度越小。

（1）简单平均差，适用于未分组资料，其计算公式为

（2）加权平均差，适用于分组数列资料，其计算公式为

6.平均差是根据全部变量值计算出来的，因此对整个变量值的离散趋势有较充分的代表性。但平均差计算由于采用取离差绝对值的方法来消除正负离差之间的互相抵消，因而不适合代数方法的演算，使其应用受到限制。

7.数组中各单位标志值与其算术平均数的离差的平方称为方差（variance），用σ2表示。方差的平方根称为标准差（standard deviation），也称均方差，用σ 表示。标准差反映分布数列中各单位标志值的一般离散水平。

（1）简单标准差

（2）加权标准差

8.标准差的特点：①便于代数运算；②离差平方和最小；③灵敏度高；④夸大差异程度。

9.离散系数也称标志变动系数，是变异指标与平均指标之比所得的相对数，反映总体各单位标志值的相对离散程度，最常用的是标准差与算术平均数对比所得的离散系数，称作“标准差系数”，用Vσ表示，其计算公式为Vσ=×100%，Vσ代表离散系数。

10.如果两个总体或数列性质不同，计量单位不同或平均水平不同，就不能采用前述的某一变异指标直接比较其离差的大小，而应分析变异指标的相对指标，即离散系数。离散系数越大，总体各单位离散的相对程度越大，平均数的代表性越差；离散系数越小，总体各单位离散的相对程度越小，平均数的代表性越好。

11.是非标志是指总体中所有单位按某种变异标志划分为具有某种属性和不具有某种属性两类，即“是”与“非”两类。是非标志值只取两个值——“是”取“1”，“非”取“0”。(www.daowen.com)

12.总体单位数为n，取值为“1”的总体单位数用n1表示，其比重（又称成数）用p 表示；取值为“0”的单位数用n0表示，其比重用q 表示，则。

13.是非标志值的标准差。

14.偏度就是次数分布的相对偏斜程度，也是总体各标志值次数分布的非对称程度，记作SKp。在次数分布完全对称的情况下，算术平均数、中位数和众数三者相等；而在偏态分布中，算术平均数、中位数和众数的数值存在差异。如果次数分布在中位数两边并不完全对称，称为偏态分布。偏态分布分为右偏分布和左偏分布。右偏分布时，算术平均数大于众数，又称正偏分布；左偏分布时，算术平均数小于众数，又称负偏分布。

15.偏态绝对量=算术平均数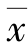（ ）-众数（Mo）。

算术平均数与众数的距离越大，偏态的绝对量越大，表示次数分布的非对称程度越大；算术平均数与众数的距离越小，偏态的绝对量越小，表示次数分布的非对称程度越小。

16.偏态系数是偏态的绝对量与其标准差之比，用SKp表示。偏态系数是从相对数上表明偏态程度，又称偏度，SKp=，SKp绝对值越大，表示偏度越大；SKp绝对值越小，表示偏度越小。偏态系数SKp的取值为[-3，3]，取值为正值时，属于正偏；取值为负值时，属于负偏。

17.统计学上经常使用中心动差来测定次数分布的偏斜或尖峭程度。三阶中心动差m3通常是测定偏态系数的一个重要指标。其公式为

式中α 代表动差法的偏态系数，即偏度。越大，表示偏度越大；越小，表示偏度越小。当α=0 时为对称分布。当α<0 时，分布呈左偏态或负偏态（值越小，说明负偏的程度越大）。当α>0 时，分布呈右偏态或正偏态（值越大，说明正偏的程度越大）。

18.峰度就是测定次数分布曲线顶端的尖峭或扁平程度的指标。当次数分布数列的次数比较集中于众数的位置，使次数分布曲线的顶部较正态分布曲线更为陡峭，属于尖顶峰度；当次数分布数列的次数在众数的位置比较分散，使分布曲线的峰顶较正态分布曲线更为平滑的，属于平顶峰度；当次数分布曲线与正态分布曲线完全相同的，属于正态峰度。峰度的公式为

当β=3 时，次数分布曲线为正态曲线；

当β<3 时，次数分布曲线为平顶曲线；

当β>3 时，次数分布曲线为尖顶曲线。

β 值越小，次数分布曲线顶端越平坦；β 值越大，次数分布曲线顶端越尖峭。