一、单选题

1.众数是总体中下列哪项的标志值。（　）

A.位置居中　B.数值最大　C.出现次数较多　D.出现次数最多

2.某工厂新工人月工资4 000 元，月工资总额200 000 元，老工人月工资8 000 元，月工资总额80 000 元，则该厂工人的平均工资为（　）。

A.6 000 元　B.5 333.3 元　C.4 666.7 元　D.5 000 元

3.平均指标反映了（　）。

A.总体次数分布的集中趋势　B.总体分布的特征

C.总体单位的集中趋势　D.总体次数分布的集中趋势

4.某企业2018年上半年月产量分别为410万、420万、380万、410万、420万、420万件，则该企业上半年的平均月产量、中位数和众数分别为（　）。

A.410万、420万、420万　B.420万、420万、420万

C.410万、415万、420万　D.415万、420万、410万

5.一组数据从小到大排序后处于中间位置上的变量值称为（　）。

A.众数　B.四分位数　C.中位数　D.平均数

6.已知某超市四种水果的销售单价和销售数量，计算这四种水果的平均价格应用（　）。

A.加权算术平均法　B.加权调和平均法

C.简单算术平均法　D.几何平均法

7.算术平均数的数学性质中，各单位标志值与平均数离差平方之和等于（　）。

A.0　B.最小值　C.1　D.各标志值之和

8.四分位距是（　）。

A.上四分位数减下四分位数的结果　B.下四分位数减上四分位数的结果

C.上四分位数减中位数　D.下四分位数减中位数

9.某服装公司为了解某类服装的代表性尺寸，最适合的指标是（　）。

A.中位数　B.众数　C.算术平均数　D.几何平均数

10.一种数据中出现频数最多的变量值称为（　）。

A.中位数　B.平均数　C.众数　D.四分位数

11.下列不受极端值影响的平均数是（　）。

A.算术平均数　B.调和平均数　C.几何平均数　D.中位数

12.在哪种条件下，简单算术平均数与加权算术平均数计算结果一致。（　）

A.权数不相等　B.权数相等　C.变量值相等　D.变量值不相等

13.从一批产品中随机抽取100 件进行质量检验，结果发现5件不合格，样本合格率的平均数及标准差为（　）。

14.用同一组数据计算的算术平均数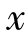 、几何平均数xG和调和平均数xH的关系是（　）。

15.（　）是一种位置平均数，它不受极大值和极小值的影响，具有稳定性特点。

A.中位数　B.众数　C.平均数　D.极差

二、多选题

1.根据标志值在总体中所处的特殊位置确定的平均指标有（　）。

A.算术平均数　B.调和平均数　C.几何平均数　D.众数

E.中位数

2.影响加权算术平均数的因素有（　）。

A.总体标志总量　B.分配数列中各组标志值

C.各组标志值出现的次数　D.各组单位数占总体单位数比重(www.daowen.com)

E.权数

三、判断题（正确的打“√”，错误的打“×”，并填写在题后的括号中）

1.权数对算术平均数的影响作用只表现为各组出现次数的多少，与各组次数占总次数的比重无关。　（　）

2.相较于算术平均数，中位数更易受到极端值的影响。　（　）

3.众数是一种数值平均数，它是指总体中出现次数最多的标志值。　（　）

4.当总体单位数n为奇数时，中位数=（n+1）/2。　（　）

5.任一组数据的众数都是唯一的。　（　）

6.三种数值平均数中调和平均数的应用范围最广，且不受变量取值的限制。　（　）

7.在一个变量数列中，中位数把全部标志值分成两个部分，即两端的标志值个数相等。（　）

8.众数不受极端变量值的影响。　（　）

9.运用平均指标时可以不考虑总体的同质性。　（　）

10.算术平均数只适合于正态分布。　（　）

四、简答题

1.什么是平均指标？它在统计分析中的作用有哪些？如何分类？

2.如何理解权数的意义？试举一则加权平均数计算实例，说明权数在其中的作用。

3.加权算术平均数与简单算术平均数有何异同点？

4.什么是众数和中位数？两者各有什么特点？

5.简述众数、中位数、算术平均数的关系。

6.正确运用平均指标的原则有哪些？

7.试述算术平均数的数学性质，并证明。

8.证明各组标志值与相应的频率之积之和等于加权算术平均数。

9.平均指标与强度指标有什么区别？

10.总量指标、相对指标、平均指标有何区别与联系？

11.数值平均数与位置平均数有何区别与联系？

五、计算题

1.某商店按销售额分组的变量数列见表1，求人均日销售额。

表1　某商店日营业额

2.已知某市25 个企业的工人平均工资见表2，计算该市工人的平均工资。

表2　某市25 个企业的工人平均工资

3.将每个数据减去60 后再缩小为原来的1/10，同时将权数缩小为原来的1/20，所求得的平均数为0.5。计算原数据的平均数。

4.某产品在3 个市场的价格及销售资料见表3，以销售额为权重求商品价格的调和平均数，以销售量为权重求商品价格加权算术平均数，试比较两种方法计算的结果，并证明调和平均数是加权算术平均数的变形。

表3　同种商品在3 个市场的销售资料

5.某地区城镇居民家庭人均收入情况见表4，计算该地区城镇居民人均收入的众数与中位数。

表4　某地区城镇居民家庭人均收入

6.根据表5 中的资料，计算车间工人定额完成程度的众数与中位数。

表5　按定额完成情况统计表

7.证明：当fm-1=fm+1时，众数等于众数组的组中值；

当fm-1>fm+1时，众数小于众数组的组中值；

当fm-1<fm+1时，众数大于众数组的组中值。