在中学平面几何中，有这样一个著名的命题：

过一圆的弦AB的中点M引任意两弦CD和EF连接CF和ED交AB于Q、P。

求证：PM＝MQ。

由于题目的图形象一只蝴蝶，因此后人给它取名为“蝴蝶定理”。

这个题最早出现在公元1815年西欧的一本通俗杂志«男士日记»上，登出来是为了征求证明。

登出的当年，英国一个自学成才的中学数学教师霍纳就给出了第一个证明。不过，霍纳的证明比较繁，使用的知识也比较深。

158年以后的1973年，又一位中学教师斯特温利用三角形面积关系，给出了一个漂亮而简捷的证明。从这以后，这个定理限于初等数学，甚至只限于初中数学的证明像雨后春笋般脱颖而出，证法多得不枚胜举。下面仅举四例与读者共同欣赏。

证法一：（斯特温法）如图，设AM＝MB＝a，MQ＝x，PM＝y。又设△EPM、△CMQ、△FMQ、△DMP的面积分别为S1、S2、S3、S4。

因为∠E＝∠C，∠D＝∠F，∠CMQ＝∠PMD，∠FMQ＝∠PME，

所以有

就是PE·DP·（MQ）2＝CQ·FQ·（MP）2。

由相交弦定理有

CQ·FQ＝BQ·QA

＝(a－x)(a＋x)

＝a2－x2,

PE·DP＝AP·PB

＝(a－y)(a＋y)

＝a2－y2,

所以有（a2－y2）x2＝（a2－x2）y2，

即a2y2＝a2x2，

∵x、y都是正数，

∴x＝y,

即PM＝MQ。

这就是斯特温的证明方法。

证法二：（反证法）仍采用证法一的各种记法。

假设QM＞MP，即x＞y。

这时有a2－x2＜a2－y2，

即AQ·BQ＜BP·AP。

根据相交弦定理，就有

CQ·FQ＜EP·DP。(1)

由正弦定理，有

将它们代入（1），化简得（QM）2＜（PM）2，(www.daowen.com)

这与假设QM＞PM矛盾。

同理可证QM＜PM不可能。

∴QM＝PM。

证法三：（三角法）如图。

设MQ＝x，MP＝y，其余如图所示。

在△EPM中，由正弦定理。（1）

在△PMD中，MP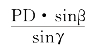＝。（2）

（1）×（2），得。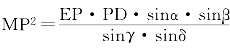

同理，。

∴,

即。

从而得

x＝y,

即MP＝MQ。

证法四：（四点共圆法）

如图，作OG⊥CF，OH⊥DE，则垂足G、H分别为CF、DE的中点，且M、Q、G、O四点共圆；M、O、H、P四点共圆。

连　接OQ、OM、MG、OP、MH。

又令∠MOQ＝∠1，∠MOP＝∠2，∠MGQ＝∠3，∠MHP＝∠4。

于是∠1＝∠3，∠2＝∠4。

又△MCF∽△MED，G、H为FC、DE的中点，

∴ ,

∴△MFG∽△MHD。

∴∠3＝∠4,

∴∠1＝∠2,

从而可得MP＝MQ。

有趣的“蝴蝶定理”磨练着无数数学爱好者的毅力和才华，历史名题，像颗颗钻石反射着人类智慧的光芒。执着的人们，不仅追求构思巧妙的解法，而且还追求变化、延伸和推广。“蝴蝶定理”的有趣，还在于它的变形和推广。

变形定理：过一圆的弦AB的中点M，引任意两条不相等的弦CD、EF，连接CE、FD并延长与AB的延长线分别交于H、G，则HM＝GM。

有兴趣的读者可以尝试证明它。

推广定理（坎迪定理）设AB是某个圆的一条弦，通过AB上任意一点M作两条弦CD和EF，连接ED、CF分别交AB于P和Q。若令AM＝a，MB＝b，QM＝x，PM＝y，求证： 。

令人惊奇的是，蝴蝶定理中的圆改为椭圆，可进一步推广为“椭圆蝴蝶定理”，而且它的逆定理也成立。有兴趣的读者可作进一步的研究。