因为盖房子要开窗户，窗子多数是矩形的，所以，建筑学家很早就研究过什么样的矩形最美。经过调查研究，大家认为，如果一个矩形，把它切掉一个正方形后，剩下的小矩形和原来的矩形相似，这样的矩形看起来才是最美的。

怎样达到这个要求呢？数学家来解决这个问题。

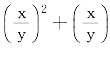如图，设矩形长为y，宽为x。要从矩形ABCD中切掉一个正方形CDFE，使矩形ABEF相似于矩形BCDA，必须也只须，也就是－1＝0。

设，解方程λ2＋λ－1＝0，得到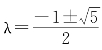，取正根，即得

这个最“美”的矩形的宽与长之比就是黄金比。

你如果留心看建筑物上的窗户，就会发现，大多数窗户像上面的矩形，而且常常分成两块，下面差不多是正方形。

把一条线段AB分成大小不等的两段AC、BC，使小段BC与大段AC的比等于大段与原线段的比，这个相等的比值、就称为黄金比，也叫做黄金数或金数，也称为黄金率，又叫中外比，这种分割方式叫黄金分割或弦分割。

古人认为，这比值极具美学价值。例如人体躯干宽与高之比近似黄金比，显得协调匀称；一张图画或照片，宽与长之比大体等于黄金比，便给人以美的感觉；窗户的宽与高之比接近黄金比，看上去美观和谐。可能是黄金比的比值适合人类的审美观，前人才以黄金冠其名。

如果AB是一根琴弦，在C点附近弹奏，琴声最为悦耳，一般说来，管弦乐器在黄金比处，奏出的声音较为和谐。

舞台的宽如果是AB，报幕员的位置应该在哪里最好呢？站在正中间显得太呆板，站在靠边的地方，又似乎失去了平衡，而站在AB的黄金分割点，多数人看来很得体。

黄金分割在建筑、艺术、工农业生产和科学实验中，有着十分广泛的应用价值。世界上有许多美好的建筑物，都是以这个数字为比例造出来的。古希腊著名的雅典女神庙，是世界公认的最完美的建筑物之一，它的圆柱高恰好是神庙高度的0．618倍；埃菲尔应用黄金分割原理，建造了举世闻名的巴黎铁塔；意大利著名画家达·芬奇在美术方面，创作了许多稀世之宝，他自称他的作品在选择比例关系时，经常用到0．618，并首次给予这种关系为“黄金分割”的美名。19世纪末，德国著名心理学家费希纳做了十个长宽之比不同的矩形，让592个人选择其中最优美的，结果绝大多数人不约而同的选择了长宽之比为黄金比的矩形。在科学家的眼中，黄金分割有“天然合理”的意义。威尼斯数学家巴巧利称黄金分割是“神圣比例”；德国著名天文学家开普勒把黄金分割称为“神圣分割”，说它是几何学中的“珍宝”。

叫人惊奇的是某些植物的生成竟也和黄金数有关。在一支茎上生长着一层一层的绿叶，是要进行光合作用，为植物制造营养。怎样使上层的叶子尽可能少遮蔽下层叶子，使阳光得到充分的利用呢？经过人们大量的观察和分析，发现了一个奥秘：原来，叶子的分布规律，和黄金数有密切的关系。(www.daowen.com)

黄金数曾被古代的数学家认为是几何两大瑰宝之一（另一个是勾股定理）。有人认为它是人类所知道的第一个无理数。发现黄金数的人，也就是发现的人——希勃索斯。他在研究正方形的对角线与边的比以前，研究的是正五边形的边与对角线的比，正五边形的边与对角线的比恰好就是不过，毕达哥拉斯学派并没有提出黄金分割的理论和名称。后来，希腊数学家仪多克萨斯从比例论的角度，对这一方法加以研究和推广，把这种分割线段的方法叫做“中外比”。欧几里得«几何原本»中有具体的作法和证明。徐光启与利玛窦合译«几何原本»，将这一方法传入我国。清朝著名数学家梅文鼎对黄金分割进行了深入的研究，在他的«几何通解»和«几何补编»中都有关于黄金分割的详细论述。

黄金数有一个奇妙的关系。设表示黄金数，我们可以验证：

λ，λ＋1，λ＋2这三个数，一个比一个大1，老大是老二的平方，老二又是老三的倒数，这种关系颇为有趣。在无穷无尽的实数之中，相互之间有这种关系的三个数，只有这三个。人们把它们叫做“奇妙的无理数三兄弟”。

黄金数有很多用途，值得一提的是优选法。什么是优选法呢？

比如，要造一种化学药剂，只知道反应温度在0℃到100℃之间的某个温度时，产品的质量最好，怎么才能找到这个最佳温度呢？那就得在0℃到100℃之间进行试验。

做试验要花钱、花时间，花人力、物力。怎样安排试验，才能用最少的试验次数，就能找到最佳的温度呢？

优选法可以帮助我们解决这个问题。怎么解决呢？黄金数发挥了作用。

取0℃到100℃之间的两个黄金分割点38．2℃和61．8℃。先在这两个温度做试验，两次试验以后，比比哪个温度效果好。如果38．2℃效果比61．8℃效果好，从61．8℃到100℃这一段就淘汰，不用试了。当试验继续进行时，又按黄金比在0℃到61．8℃这个范围内选点，由黄金比的性质，只要取23．6℃就够了，把试验结果与38.2℃时的试验结果比较，又可以淘汰掉0℃到23．6℃和38．2℃到61．8℃这两段之一。

试一次，淘汰一段，只要做十几次试验，就可以找到最佳温度。

利用黄金数来设计试验，是1953年国外一篇文章中提出的。我国著名数学家华罗庚教授，在优选法的进一步研究中，做出了重要贡献。他第一个指出，国外数学家虽然提出了利用黄金数设计试验，但没有证明黄金分割的最优性。在他指出这一点之后不到一年，我国的青年数学家，著名的计算机科学家洪加威教授彻底解决了这个问题，证明了黄金分割的最优性。

华罗庚教授和他的得意弟子王元教授，对黄金数进行了深刻的研究和巧妙的推广，从而设计出强有力的计算多重积分的新方法，他们的这一研究成果在世界上处于领先地位，获得国际数学界的很高评价。人类认识黄金数的漫长历史，又揭开了新的辉煌的一页。