复数的乘法法则:
设z1=a+bi,z2=c+di(a,b,c,d∈R)是任意两个复数,那么它们的积(a+bi)(c+di)=ac+bci+adi+bdi2=(ac-bd)+(ad+bc)i.
复数的除法:
(1)复数除法定义:满足(c+di)(x+yi)=a+bi的复数x+yi(x,y∈R)叫复数a+bi除以复数c+di的商,记为(a+bi)÷(c+di)或者![]() .
.
(2)复数的除法法则:
方法简述
1.定义法
例1 计算: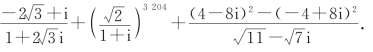
点拨 复数代数形式四则混合运算法则.
解答
反思 模的运算法则需熟练,计算需要细心.
例2 设![]() ,z2=1-i,试求满足
,z2=1-i,试求满足![]() 的最小正整数m,n的值.
的最小正整数m,n的值.
点拨 两边取模.
解答 对![]() 两边取模得
两边取模得![]() ,所以m=2n,从而
,所以m=2n,从而![]()
所以![]() ,于是n=3k(k∈N+).
,于是n=3k(k∈N+).
所以满足条件的最小正整数是m=6,n=3.
反思 ![]() ,则n=3k(k∈N+)是常见结论.
,则n=3k(k∈N+)是常见结论.
2.待定系数法
例3 是否存在复数z,使其满足![]() ,如果存在,求出z的值;如果不存在,说明理由.
,如果存在,求出z的值;如果不存在,说明理由.
点拨 复数相等可采用待定系数法求解.
解答 设z=x+yi(x,y∈R).
则x2+y2+2i(x-yi)=3+ai.∴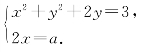
消去x,得y2+2y+![]() -3=0,Δ=16-a2.(https://www.daowen.com)
-3=0,Δ=16-a2.(https://www.daowen.com)
当且仅当|a|≤4时,复数z存在,这时![]()
反思 转化为方程组有解问题,利用判别式即可.
易错解读
例4 已知![]() ,求使(-ωi)n∈N*的最小正整数n.
,求使(-ωi)n∈N*的最小正整数n.
解答 ∵ω3=1,∴(-ωi)n=(-1)n·ωn·in,易知n=12.
易错分析 忽略(-ωi)n∈N*的条件,可能会得出n=3或n=6.
例5 已知f(x)=-x5+5x4-10x3+10x2-5x+1,求![]() 的值.
的值.
解答 ∵f(x)=-(x-1)5,∴![]() =-ω2=-
=-ω2=-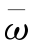 =
=![]() .
.
易错分析 注意观察解析式的结构特点,不能直接代入,否则十分烦琐.
经典训练
1.计算:![]()
2.复数![]() 等于( ).
等于( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.求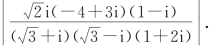
4.已知![]() 是纯虚数,求z在复平面内对应点的轨迹.
是纯虚数,求z在复平面内对应点的轨迹.
5.设z为复数,M={z|(z-1)2=|z-1|2},那么( ).
A.M={纯虚数} B.M={实数}
C.{实数}⊂M⊂{复数} D.M={虚数}
6.若f(z)=2z+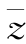 -3i,f(
-3i,f( +i)=6-3i,试求f(-z).
+i)=6-3i,试求f(-z).
7.(1)已知z1,z2∈C,求证:![]()
(2)已知z1,z2∈C,且![]() .求证:
.求证:![]() 中至少有一个是1.
中至少有一个是1.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






