设复数z1=a+bi,z2=c+di,在复平面上所对应的向量为的坐标形式为为邻边作平行四边形OZ1ZZ2,则对角线OZ对应的向量是,所以,这说明两个向量的和就是与复数(a+c)+(b+d)i对应的向量.因此,复数的加法就可以按照向量的加法来进行,这就是复数加法的几何意义.复数减法的几何意义同复数加法的几何意义类似.

方法简述

1.定义法

例1 已知z1=a+bi,z2=c+di(a,b,c,d∈R),若z1+z2是纯虚数,则有(　).

A.a-c=0且b-d≠0　B.a-c=0且b+d≠0

C.a+c=0且b-d≠0　D.a+c=0且b+d≠0

点拨 z1+z2=(a+c)+(b+d)i.

因为z1+z2为纯虚数,所以a+c=0且b+d≠0.

解答 D

反思 复数的加法运算法则.

例2 设f(z)=z-2i,z1=3+4i,z2=-2-i,则f(z1-z2)=(　).

A.1-5i　B.-2+9i　C.-2-i　D.5+3i

点拨 ∵z1-z2=(3+4i)-(-2-i)=5+5i,

∴f(z1-z2)=5+5i-2i=5+3i.

解答 D

反思 复数的减法运算法则.

2.数形结合思想

例3 若|z-1|=|z+1|,则|z-1|的最小值是_________.

点拨 可以利用复数的几何意义或者待定系数法求解.

解答 解法一:因为|z-1|=|z+1|,

例3答图

所以z的轨迹为以A(1,0),B(-1,0)为端点的线段的垂直平分线,即y轴.

|z-1|表示y轴上的点到(1,0)的距离,所以最小值为1,如图所示.

解法二:设z=a+bi(a,b∈R),

则|(a-1)+bi|=|(a+1)+bi|.

∴

即a=0.∴z=bi,b∈R.

∴|z-1|min=|bi-1|min=

故当b=0时,|z-1|的最小值为1.

反思 利用复数的几何意义求解更为简洁明了.

易错解读

例4 已知复数z满足z+|z|=2+8i.求复数z.

解答 解法一:设z=a+bi(a,b∈R).(www.daowen.com)

将代入方程,得

则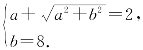解得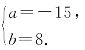

即z=-15+8i.

解法二:原式可化为z=2-|z|+8i.

∵|z|∈R,∴2-|z|是z的实数.

∴,即|z|2=68-4|z|+|z|2.

解得|z|=17.代入z=2-|z|+8i,得z=-15+8i.

易错分析 复数的模公式代错.

例5 已知|z1|=|z2|=|z1-z2|=1,求|z1+z2|.

解答 解法一:设z1=a+bi,z2=c+di(a,b,c,d∈R).

∵|z1|=|z2|=|z1-z2|=1,

∴a2+b2=c2+d2=1. ①

(a-c)2+(b-d)2=1. ②

由①②,得2ac+2bd=1.

解法二:设O为坐标原点,

则z1,z2,z1+z2对应的复数分别为A,B,C.

∵|z1|=|z2|=|z1-z2|=1,

∴△OAB是边长为1的正三角形,

∴四边形OACB是一个内角为60°,边长为1的菱形,

且|z1+z2|是菱形的较长的对角线OC的长.

∴|z1+z2|=|OC|=

易错分析 不能快速找到本题的切入点,对于解法二不能正确理解复数模的几何意义.

经典训练

1.如图所示,平行四边形OABC,顶点O,A,C分别表示0,3+2i,-2+4i,试求:

第1题图

(1)所表示的复数,所表示的复数;

(2)对角线所表示的复数;

(3)对角线所表示的复数及的长度.

2.复数z1=1+2i,z2=-2+i,z3=-1-2i,它们在复平面上的对应点是一个正方形的三个顶点,求这个正方形的第四个顶点对应的复数.

3.已知z1=a2-3+(a+5)i,z2=a-1+(a2+2a-1)i(a∈R)分别对应向量(O为原点),若向量对应的复数为纯虚数,求a的值.

4.,求2z+3-4i对应的点的轨迹方程.

5.设复数满足,求的最大值和最小值.