复数集C和复平面内所有点所成的集合是一一对应关系,即复数复平面内的点Z(a,b),这是因为,每一个复数有复平面内唯一的一个点和它对应;反过来,复平面内的每一个点,有唯一的一个复数和它对应.这就是复数的一种几何意义.也就是复数的另一种表示方法,即几何表示方法.

方法简述

1.等价转化思想

例1 在复平面上,设点A,B,C,对应的复数分别为i,1,4+2i.过A,B,C作平行四边形ABCD,求此平行四边形的对角线BD的长.

点拨 把复数在复平面上对应的点坐标表示出来,再利用平行四边形性质即可求解.

解答 由题知平行四边形三顶点坐标为A(0,1),B(1,0),C(4,2).

设D点的坐标为D(x,y).

由,得(-1,1)=(x-4,y-2).

所以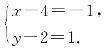

解得即D(3,3).

所以,则

反思 通过平行四边形的三个点求出第四个点.

2.数形结合思想

例2 若复数z满足条件,求的最值.

点拨 本题的方法很多,可以用多种方法解答.

解答 解法一:(数形结合法)

由可知,z对应于单位圆上的点z;表示单位圆上的点z到点P(0,2)的距离,如图所示.

例2答图

当点z运动到A(0,1)点时,,此时z=i;

当点z运动到B(0,-1)点时,,此时z=-i.

解法二:(不等式法)

∵

∴

∵

解法三:(代数法)

设z=x+yi(x,y∈R),则x2+y2=1.

∴

∵,即-1≤y≤1,

∴当y=1,即z=i时,

解法四:(性质法)

设z=x+yi(x,y∈R).

∵,即-1≤y≤1,

∴当y=1,即z=i时,

当y=-1,即z=-i时,

反思 体会不同方法的解题区别.(www.daowen.com)

例3 复数z满足条件,则复数z所对应的点Z的轨迹是(　).

A.双曲线　B.双曲线的右支　C.线段　D.射线

点拨 条件表示复平面上的点Z到(0,-2)与(0,2)的距离之差为4的点的轨迹.

解答 一条射线,故选D.

反思 条件中隐藏的复数几何意义要弄清楚.

易错解读

例4 已知z1,z2∈C,且,若z1+z2=2i,则的最大值是(　).

A.6　B.5　C.4　D.3

解答 解法一:

∵的最大值是4,故选C.

解法二:∵z1+z2=2i,∴z1=2i-z2.

∵,即

∵表示以原点为圆心,以1为半径的圆;表示以(0,2)为圆心,以1为半径的圆.

∴的最大值为两圆上距离最大的两点间的距离为4.故选C.

易错分析 该题如果用代数法求解,问题不仅变复杂而且易计算出错,充分利用模的不等式,通过构造关于的不等式,达到解题目的.

解法二则是运用复数的几何性质,通过数形结合,充分利用图形的直观、形象的特点,化简了对问题的处理方法,也是不容易想的,更是易错之处.

经典训练

1.若,则复数(cosθ+sinθ)+(sinθ-cosθ)i在复平面内所对应的点在(　).

A.第一象限　B.第二象限　C.第三象限　D.第四象限

2.已知复数z1=cosθ-i,z2=sinθ+i,求|z1·z2|的最大值和最小值.

3.满足条件|z-i|=|3+4i|的复数z在复平面上对应点的轨迹是(　).

A.一条直线　B.两条直线　C.圆　D.椭圆

4.在复平面内,把复数对应的向量按顺时针方向旋转,所得向量对应的复数是(　).

A.　B.　C.　D.

5.已知复数z的模为2,则|z-i|的最大值为(　).

A.1　B.2　C.　D.3

6.若z∈C且|z+2-2i|=1,则|z-2-2i|的最小值是(　).

A.2　B.3　C.4　D.5

7.若a,b为非零实数,则下列四个命题都成立:

①a+≠0 ②a+b　2=a2+2ab+b2 ③若,则a=±b ④若a2=ab,则a=b,

则对于任意非零复数a,b,上述命题仍然成立的序号是________.

8.在复数范围内解方程(i为虚数单位).