理解并掌握虚数单位i以及实数、虚数、纯虚数、共轭复数、实部、虚部等相关概念.
复数相等的充要条件:若在复数集![]() 中任取两个数a+bi,c+di(a,b,c,d∈R),则它们相等的充要条件是a=c,b=d,两个复数除都是实数外,不能比较大小,只有相等关系.
中任取两个数a+bi,c+di(a,b,c,d∈R),则它们相等的充要条件是a=c,b=d,两个复数除都是实数外,不能比较大小,只有相等关系.
方法简述
1.基本定义
例1 设x∈R,则“x=1”是“复数z=(x2-1)+(x+1)i为纯虚数”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
点拨 复数为纯虚数的条件:实部为零,虚部不为零.
解答 由纯虚数的定义,知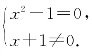 解得x=1.故选C.
解得x=1.故选C.
反思 充要条件的理解.
2.待定系数法
例2 若复数z满足z(1+i)=1-i(i是虚数单位),则其共轭复数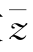 =_________.
=_________.
点拨 共轭复数的定义.
解答 设z=a+bi,则(a+bi)(1+i)=1-i,即a-b+(a+b)i=1-i.
由![]() 解得
解得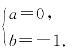
所以z=-i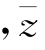 =i.
=i.
反思 利用复数相等求出z,进而求出z-.
例3 设a,b为共轭复数,且(a+b)2-3abi=4-12i,求a,b的值.
点拨 两个复数相等的条件:实部、虚部分别相等.
解答 设a=x+yi,b=x-yi(x,y∈R).
代入原方程,得4x2-3(x2+y2)i=4-12i,
由复数相等的条件,得
解得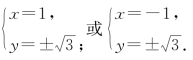
故![]() 或
或![]()
或![]() 或
或![]()
反思 共轭复数的概念以及待定系数法.
易错解读
例4 已知z,w为复数,(1+3i)·z为纯虚数,w=![]() ,且
,且![]() ,求复数w.
,求复数w.
解答 设z=x+yi(x,y∈R),则(1+3i)·z=(x-3y)+(3x+y)i为纯虚数.
所以x-3y=0,3x+y≠0.因为![]() ,所以
,所以![]()
又x=3y≠0,解得x=15,y=5或x=-15,y=-5,所以![]()
易错分析 容易造成漏解情况.
例5 z=x+yi(x,y∈R),且2x+y+ilog2x-8=(1-log2y)i,求z.
解答 ∵2x+y+ilog2x-8=(1-log2y)i,
∴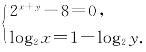 解得
解得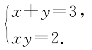
解得![]()
∴z=2+i或z=1+2i.
易错分析 对题目的理解出问题,造成解答出错.
例6 关于x的方程x2-(tanθ+i)x-(2+i)=0;若方程有实数根,求锐角θ和实数根.
解答 设实数根是a,则a2-(tanθ+i)a-(2+i)=0.(https://www.daowen.com)
整理,得a2-atanθ-2-(a+1)i=0.
∵a,tanθ∈R,∴
∴a=-1且tanθ=1.又0<θ<![]() ,∴θ=
,∴θ=![]() ,a=-1.
,a=-1.
易错分析 解题过程中出现一元二次方程,若通过求解Δ来解决问题,则会出现困难.
经典训练1.在复平面内表示复数i(1-2i)的点位于( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.设i是虚数单位,z-表示复数z的共轭复数,若z=1+i,则![]() +i·
+i·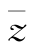 =( ).
=( ).
A.-2 B.-2i C.2 D.2i
3.复数z=(3-2i)i的共轭复数z-等于( ).
A.-2-3i B.-2+3i C.2-3i D.2+3i
4.已知复数z满足(3-4i)z=25则z=( ).
A.3-4i B.3+4i C.-3-4i D.-3+4i
5.满足![]() =i(i为虚数单位)的复数z=( ).
=i(i为虚数单位)的复数z=( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设复数z满足(z-2i)(2-i)=5,则z=( ).
A.2+3i B.2-3i C.3+2i D.3-2i
7.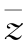 是z的共轭复数.若z+
是z的共轭复数.若z+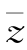 =2,(z-
=2,(z-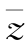 )i=2(i为虚数单位),则z=( ).
)i=2(i为虚数单位),则z=( ).
A.1+i B.-1-i C.-1+i D.1-i
8.i是虚数单位,复数![]() =( ).
=( ).
A.1-i B.-1+i C.![]() D.
D.![]()
9.已知a,b∈R,i是虚数单位,若a-i与2+bi互为共轭复数,则(a+bi)2=( ).
A.5-4i B.5+4i C.3-4i D.3+4i
10.原命题为“若z1,z2互为共轭复数,则![]() ”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( ).
”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是( ).
A.真,假,真 B.假,假,真 C.真,真,假 D.假,假,假
11.已知i是虚数单位,a,b∈R,则“a=b=1”是“(a+bi)2=2i”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
12.i为虚数单位,![]() =( ).
=( ).
A.-1 B.1 C.-i D.i
13.![]() =( ).
=( ).
A.1+i B.1-i C.-1+i D.-1-i
14.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=2+i,则z1z2=( ).
A.-5 B.5 C.-4+i D.-4-i
15.复数![]() =________.
=________.
16.设![]() ,则z的共轭复数为( ).
,则z的共轭复数为( ).
A.-1+3i B.-1-3i C.1+3i D.1-3i
17.复数![]() =_________.
=_________.
18.若复数z=1+2i,其中i是虚数单位,则![]() =_______________.
=_______________.
19.已知复数z=(5-2i)2(i为虚数单位),则z的实部为________.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







