1.空间向量的直角坐标运算
设![]() ,则
,则
(1)![]()
(2)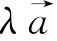 =(λa1,λa2,λa3)(λ∈R);
=(λa1,λa2,λa3)(λ∈R);
(3)![]() =a1b1+a2b2+a3b3;
=a1b1+a2b2+a3b3;
(4)![]()
(5)![]()
(6)![]()
(用到常用的向量模与向量之间的转化:![]()
(7)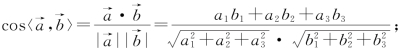
(8)设A(x1,y1,z1),B(x2,y2,z2),则![]() =(x2,y2,z2)-(x1,y1,z1)=(x2-x1,y2-y1,z2-z1).
=(x2,y2,z2)-(x1,y1,z1)=(x2-x1,y2-y1,z2-z1).
这就是说,一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去始点的坐标.则![]() ,这就是空间两点间的距离公式.
,这就是空间两点间的距离公式.
2.法向量
若向量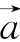 所在直线垂直于平面α,则称这个向量垂直于平面α,记作
所在直线垂直于平面α,则称这个向量垂直于平面α,记作![]() ,如果
,如果![]() ,那么向量
,那么向量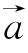 叫作平面α的法向量.法向量的用法如下:
叫作平面α的法向量.法向量的用法如下:
(1)利用法向量可求点到平面的距离定理:如图(a)所示,设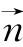 是平面α的法向量,AB是平面α的一条射线,其中A∈α,则点B到平面α的距离为
是平面α的法向量,AB是平面α的一条射线,其中A∈α,则点B到平面α的距离为![]() (实质是
(实质是![]() 在法向量
在法向量![]() 方向上的投影的绝对值).
方向上的投影的绝对值).
(2)利用法向量可求二面角的平面角定理:如图(b)所示,设![]() 分别是二面角α-l-β中平面α,β的法向量,则
分别是二面角α-l-β中平面α,β的法向量,则![]() 所成的角就是所求二面角的平面角或其补角大小.二面角α-l-β的平面角
所成的角就是所求二面角的平面角或其补角大小.二面角α-l-β的平面角![]() 为平面α,β的法向量).
为平面α,β的法向量).
(3)如图(c)所示,直线AB与平面α所成角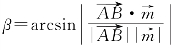
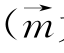 为平面α的法向量).
为平面α的法向量).
(4)如图(d)所示,异面直线l1,l2间的距离![]() (l1,l2的公垂向量为
(l1,l2的公垂向量为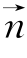 ,C,D分别是l1,l2上任一点,d为l1,l2间的距离)(实质是
,C,D分别是l1,l2上任一点,d为l1,l2间的距离)(实质是![]() 在公垂向量
在公垂向量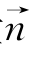 方向上的投影的绝对值).
方向上的投影的绝对值).
方法简述
例1图
1.建立空间直角坐标系
例1 如图所示,在正方体ABCD-A1B1C1D1中,M、N分别是C1C,B1C1的中点.求证:MN∥平面A1BD.
点拨 直接用线面平行定理不易证明,考虑用向量方法证明.
证明 证法一:如图所示,以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,设正方体的棱长为1,则![]() ,D(0,0,0),A1(1,0,1),B(1,1,0),于是
,D(0,0,0),A1(1,0,1),B(1,1,0),于是![]()
例1答图
设平面A1BD的法向量是![]()
则![]() ,且
,且![]() ,得
,得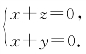
取x=1,得y=-1,z=-1.∴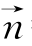 =(1,-1,-1).
=(1,-1,-1).
又![]()
∴![]() 又MN⊄平面A1BD,
又MN⊄平面A1BD,
∴MN∥平面A1BD.
证法二![]()
∴![]() 又MN与DA1不共线,∴MN∥DA1.
又MN与DA1不共线,∴MN∥DA1.
又MN⊄平面A1BD,A1D⊂平面A1BD,
∴MN∥平面A1BD.
反思 证明直线与平面平行,只需证明直线的方向向量与平面的法向量的数量积为零,或证直线的方向向量与平面内的不共线的两个向量共面,然后说明直线在平面外即可.这样就把几何的证明问题转化为向量的计算问题.
例2图
例2 如图所示,在棱长为1的正方体OABC-O1A1B1C1中,E,F分别是棱AB,BC上的动点,且AE=BF=x,其中0≤x≤1,以O为原点建立空间直角坐标系O-xyz.
(1)求证:A1F⊥C1E;
(2)若A1,E,F,C1四点共面,求证![]()
点拨 本题已建好空间直角坐标系,故可用向量法求解,要注意找准点的坐标.
证明 (1)由已知条件,知
A1(1,0,1),F(1-x,1,0),C1(0,1,1),E(1,x,0),
则![]()
∴![]()
∴![]() 即A1F⊥C1E.
即A1F⊥C1E.
(2)由已知条件,知![]()
![]()
设![]() ,则
,则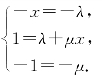
解得![]()
∴![]()
反思 证明直线与直线垂直,只需要证明两条直线的方向向量垂直,而直线与平面垂直,平面与平面垂直可转化为直线与直线垂直的证明.
例3图
例3 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=![]() ,M,N分别为AB,SB的中点,如图所示,求点B到平面CMN的距离.
,M,N分别为AB,SB的中点,如图所示,求点B到平面CMN的距离.
点拨 考虑用向量法求距离,距离公式不要记错.
解答 取AC的中点O,联结OS,OB.
∵SA=SC,AB=BC,
∴AC⊥SO,AC⊥BO.
∵平面SAC⊥平面ABC,平面SAC∩平面ABC=AC,
∴SO⊥平面ABC,∴SO⊥BO.
例3答图
如图所示,建立空间直角坐标系O-xyz,
则![]() ,C(-2,0,0),S(0,0,
,C(-2,0,0),S(0,0,![]() ),
),![]()
∴![]()
![]()
设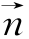 =(x,y,z)为平面CMN的一个法向量,
=(x,y,z)为平面CMN的一个法向量,
则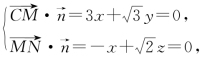 取z=1,
取z=1,
则![]()
∴点B到平面CMN的距离为![]()
反思 点到平面的距离,利用向量法求解比较简单,它的理论基础仍基于几何法.如本题,事实上,作BH⊥平面CMN于H.由![]()
得![]() ,所以
,所以![]()
例4图
例4 如图所示,已知点P在正方体ABCD-A'B'C'D'的对角线B'D'上,∠PDA=60°.
(1)求DP与CC'所成角的大小;
(2)求DP与平面AA'D'D所成角的大小.
点拨 建立空间直角坐标系,利用空间向量求解.
解答 如图所示,以D为原点,DA为单位长建立空间直角坐标系D-xyz.
则![]() 联结BD,B'D'.
联结BD,B'D'.
在平面BB'D'D中,延长DP交B'D'于H.
设![]() ,由已知
,由已知![]() 由
由![]() ,可得
,可得![]()
例4答图
解得![]() ,所以
,所以![]()
(1)因为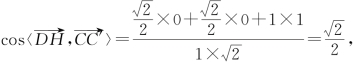 所以
所以![]() ,即DP与CC'所成的角为45°.
,即DP与CC'所成的角为45°.
(2)平面AA'D'D的一个法向量是![]()
因为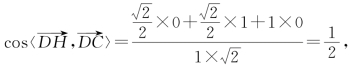
所以![]() ,可得DP与平面AA'D'D所成的角为30°.
,可得DP与平面AA'D'D所成的角为30°.
反思 注意线线角、线面角的范围.
例5 已知一四棱锥P-ABCD的三视图如图所示,E是侧棱PC上的动点.
(1)求四棱锥P-ABCD的体积.
(2)是否不论点E在何位置,都有BD⊥AE?证明你的结论.
(3)若点E为PC的中点,求二面角D-AE-B的大小.
例5图
点拨 由三视图可得出空间几何体.
解答 (1)由该四棱锥的三视图可知,该四棱锥P-ABCD的底面是边长为1的正方形,侧棱PC⊥底面ABCD,且PC=2.∴VP-ABCD=![]()
(2)不论点E在何位置,都有BD⊥AE.
证明:联结AC,∵ABCD是正方形,∴BD⊥AC.
∵PC⊥底面ABCD且BD⊂平面ABCD,∴BD⊥PC.
又AC∩PC=C,∴BD⊥平面PAC.
∵不论点E在何位置,都有AE⊂平面PAC.
∴不论点E在何位置,都有BD⊥AE.
例5答图
(3)解法一:在平面DAE内过点D作DG⊥AE于G,联结BG.
∵CD=CB,EC=EC,∴Rt△ECD≌Rt△ECB,∴ED=EB.
∵AD=AB,∴△EDA≌△EBA,∴BG⊥EA.
∴∠DGB为二面角D-EA-B的平面角.
∵BC⊥DE,AD∥BC,∴AD⊥DE.
在Rt△ADE中,DG=![]()
在△DGB中,由余弦定理得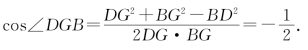
∴∠DGB=![]() ,∴二面角D-AE-B的大小为
,∴二面角D-AE-B的大小为![]() .
.
解法二:以点C为坐标原点,CD所在的直线为x轴建立空间直角坐标系如图所示,
则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),从而![]()
设平面ADE和平面ABE的法向量分别为![]()
由法向量的性质,可得-a+c=0,b=0,a'=0,-b'+c'=0.
令c=1,c'=-1,则a=1,b'=-1,∴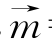 =(1,0,1)
=(1,0,1)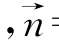 =(0,-1,-1).
=(0,-1,-1).
设二面角D-AE-B的平面角为θ,则![]()
∴θ=![]() ,∴二面角D-AE-B的大小为
,∴二面角D-AE-B的大小为![]() .
.
反思 几何法与空间向量法均可解决问题,可以体会两者的不同.
例6图
例6 如图所示,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
(1)设G是OC的中点,证明:FG∥平面BOE;
(2)证明:在△ABO内存在一点M,使FM⊥平面BOE.
点拨 以O点为原点,OB,OC,OP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,利用向量法可求解.
解答 (1)证明:如图所示,联结OP,以O为坐标原点,分别以OB,OC,OP所在直线为x轴,y轴,z轴,建立空间直角坐标系O-xyz,则有O(0,0,0),A(0,-8,0),B(8,0,0),C(0,8,0),P(0,0,6),E(0,-4,3),F(4,0,3).由题意,得G(0,4,0).
例6答图
因为![]() ,因此平面BOE的一个法向量
,因此平面BOE的一个法向量![]() =(0,3,4),(www.daowen.com)
=(0,3,4),(www.daowen.com)
由![]() ,得
,得![]() .又因为直线FG不在平面BOE内,所以FG∥平面BOE.
.又因为直线FG不在平面BOE内,所以FG∥平面BOE.
(2)设点M的坐标为(x0,y0,0),则![]()
因为FM⊥平面BOE,所以有![]()
因此有x0=4,y0=,即点M的坐标为![]()
在平面直角坐标系xOy中,△AOB的内部区域可表示为不等式组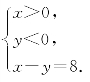
经检验,点M的坐标满足上述不等式组,
所以,在△ABO内存在一点M,使FM⊥平面BOE.
反思 (1)空间中线面的平行与垂直的证明有两种思路:一是利用相应的判定定理和性质定理去解决;二是利用空间向量法来论证.
(2)用向量法来证明平行与垂直,避免了繁杂的推理论证,直接计算就行了,把几何问题代数化.尤其是在正方体、长方体、直四棱柱中相关问题的证明用向量法会更简捷,但是向量法要求计算必须准确无误.
例7图
例7 如图所示,在三棱锥P-ABC中,PB⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC的中点.
(1)求证:BE⊥平面PAC;
(2)求二面角E-AB-C的余弦值.
点拨 本题的关键是在平面ABC内找到两条互相垂直的直线,可以过点B作BC的垂线BT,分别以BC,BT,BP为x,y,z轴建立空间直角坐标系.
解答 (1)证明:∵PB⊥平面ABC,∴PB⊥AC.又BC⊥AC,∴AC⊥平面PBC,∴AC⊥BE.
又PB=BC,且E为中点,∴BE⊥PC,∴BE⊥平面PAC.
例7答图
(2)如图所示,在平面ABC内过点B作BT⊥BC,分别以BC,BT,BP为x,y,z轴建立空间直角坐标系,则B(0,0,0),C(4,0,0),A(4,4,0),P(0,0,4),E(2,0,2),则![]() =(4,4,0),
=(4,4,0),![]() =(2,0,2),平面ABC的法向量为
=(2,0,2),平面ABC的法向量为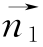 =(0,0,1).设平面ABE的法向量为
=(0,0,1).设平面ABE的法向量为![]() =(x,y,z),则
=(x,y,z),则![]() ,即
,即![]()
令z=1,得x=-1,y=1,即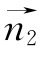 =(-1,1,1).
=(-1,1,1).
设二面角E-AB-C为θ,则![]()
反思 利用空间向量坐标运算求空间角的一般步骤为:(1)建立恰当的空间直角坐标系;(2)求出相关点的坐标;(3)写出向量坐标;(4)结合公式进行论证、计算;(5)转化为几何结论.
易错解读
例8图
例8 如图所示,在直三棱柱ABC-A1B1C1中,BA=BC=2,![]()
![]() ,异面直线A1B与AC成60°的角,点O,E分别是棱AC和BB1的中点,点F是棱B1C1上的动点.
,异面直线A1B与AC成60°的角,点O,E分别是棱AC和BB1的中点,点F是棱B1C1上的动点.
(1)求证:A1E⊥OF;
(2)求点E到平面AB1C的距离;
(3)求二面角B1-A1C-C1的大小.
解答 (1)证明:设棱柱的高为h,以B为坐标原点,以BA,BC,BB1所在直线分别为x,y,z轴建立空间直角坐标系,则有B(0,0,0),A(2,0,0),C(0,2,0),O(1,1,0),A1(2,0,h).
∴![]()
∴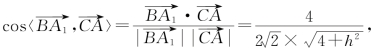 即
即![]() ,解得h=2.
,解得h=2.
例8答图
∴E(0,0,1),A1(2,0,2),∴![]() =(-2,0,-1).
=(-2,0,-1).
∵F是B1C1上的动点,
∴设F(0,y,2),∴![]() =(-1,y-1,2).
=(-1,y-1,2).
∴![]() =(-2,0,-1)·(-1,y-1,2)=0.
=(-2,0,-1)·(-1,y-1,2)=0.
∴![]() ,即A1E⊥OF.
,即A1E⊥OF.
(2)易求平面AB1C的法向量为![]()
所以E到平面AB1C的距离为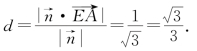
(3)平面A1CC1的一个法向量是![]() =(1,1,0).
=(1,1,0).
设平面A1B1C的一个法向量是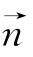 =(x,y,z).
=(x,y,z).
因为![]()
则![]() =(x,y,z)·(-2,2,-2)=-2x+2y-2z=0,①
=(x,y,z)·(-2,2,-2)=-2x+2y-2z=0,①
![]() =(x,y,z)·(-2,0,0)=-2x=0,∴x=0.②
=(x,y,z)·(-2,0,0)=-2x=0,∴x=0.②
将②代入①并令z=1得y=1,∴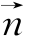 =(0,1,1).
=(0,1,1).
∴![]()
∴![]() ,即二面角B1-A1C-C1的大小为60°.
,即二面角B1-A1C-C1的大小为60°.
易错分析 本题的易错之处在于建立空间直角坐标系,合理选好坐标原点、坐标轴是解本题的关键,可使点、线表示简化,也直接影响本题的解答;另外的易错之处在于隐藏“特定”向量关系于计算之中,如:向量的数量积为零是证明空间垂直的重要工具.
例9 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD.在四边形ABCD中,AB⊥AD,AB+AD=4,![]() ,∠CDA=45°.
,∠CDA=45°.
例9图
(1)求证:平面PAB⊥平面PAD;
(2)设AB=AP.
①若直线PB与平面PCD所成的角为30°,求线段AB的长;
②在线段AD上是否存在一个点G,使得点G到点P,B,C,D的距离都相等?说明理由.
解答 (1)因为PA⊥平面ABCD,AB⊂平面ABCD,
所以PA⊥AB.
又AB⊥AD,PA∩AD=A,
所以AB⊥平面PAD.
又AB⊂平面PAB,所以平面PAB⊥平面PAD.
(2)以A为坐标原点,建立空间直角坐标系A-xyz,如图(a)所示.
例9答图(a)
在平面ABCD内,作CE∥AB交AD于点E,
则CE⊥AD.
在Rt△CDE中,DE=CD·cos45°=1,
CE=CD·sin45°=1.
设AB=AP=t,则B(t,0,0),P(0,0,t).
由AB+AD=4得AD=4-t,
所以E(0,3-t,0),C(1,3-t,0),D(0,4-t,0)![]() =(0,4-t,-t).
=(0,4-t,-t).
①设平面PCD的法向量为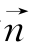 =(x,y,z).由
=(x,y,z).由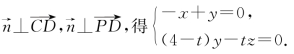
取x=t,得平面PCD的一个法向量![]() =(t,t,4-t).
=(t,t,4-t).
又![]() =(t,0,-t),
=(t,0,-t),
故由直线PB与平面PCD所成的角为30°得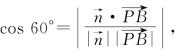
即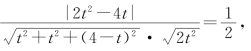
解得![]() 或t=4(舍去).因为AD=4-t>0,所以
或t=4(舍去).因为AD=4-t>0,所以![]()
例9答图(b)
②假设在线段AD上存在一个点G,使得点G到P,B,C,D的距离都相等,如图(b)所示.
设G(0,m,0)(其中0≤m≤4-t),
则![]() =(1,3-t-m,0),
=(1,3-t-m,0),![]() =(0,4-t-m,0)
=(0,4-t-m,0)![]() =(0,-m,t).
=(0,-m,t).
由![]() 得12+(3-t-m)2=(4-t-m)2,
得12+(3-t-m)2=(4-t-m)2,
即t=3-m.①
由![]() 得(4-t-m)2=m2+t2.②
得(4-t-m)2=m2+t2.②
由①②消去t,化简得m2-3m+4=0.③
由于方程③没有实数根,所以在线段AD上不存在一个点G,使得点G到点P,C,D的距离都相等.从而,在线段AD上不存在一个点G,使得点G到点P,B,C,D的距离都相等.
易错分析 (1)本题虽不难,但是表达是关键,易出错,原因是不易从现有的直线中寻找平面的垂线,即一个平面经过另一个平面的垂线,可先根据线线垂直,证明线面垂直,即可证得面面垂直.
(2)第①小题学生易用综合法,但由于题中PB与平面PCD所成的角不好作出,因此用向量法求解,易错之处在于坐标系的选择.第②小题易错之处在于反证法运用,可先假设点G存在,然后推理得出矛盾或列出方程无解,从而否定假设.
经典训练
1.已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,高AA1=2,求:
第1题图
(1)异面直线BD与AB1所成角的余弦值;
(2)四面体AB1D1C的体积.
2.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.求证:
第2题图
(1)AE⊥CD;
(2)PD⊥平面ABE.
3.如图所示,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=![]() .
.
第3题图
(1)求点A到平面MBC的距离;
(2)求平面ACM与平面BCD所成二面角的正弦值.
4.如图所示,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=![]() .
.
(1)求异面直线BF与DE所成的角的大小;
(2)求证:平面AMD⊥平面CDE;
(3)求二面角A-CD-E的余弦值.
第4题图
5.如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
(1)若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值;
(2)用反证法证明:直线ME与BN是两条异面直线.
第5题图
6.如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为BC的中点.
(1)求异面直线NE与AM所成角的余弦值;
(2)在线段AN上是否存在点S,使得ES⊥平面AMN?若存在,求线段AS的长;若不存在,请说明理由.
第6题图
7.如图所示,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(1)求证:平面AEC⊥平面PDB;
(2)当![]() 且E为PB的中点时,求AE与平面PDB所成的角的大小.
且E为PB的中点时,求AE与平面PDB所成的角的大小.
第7题图
8.如图所示,在正三棱柱ABC-A1B1C1中,AB=![]() ,D是A1B1的中点,点E在A1C1上,且DE⊥AE.
,D是A1B1的中点,点E在A1C1上,且DE⊥AE.
第8题图
(1)求证:平面ADE⊥平面ACC1A1;
(2)求直线AD和平面ABC1所成角的正弦值.
9.如图所示,在正三棱柱ABC-A1B1C1中,AB=4,AA1=![]() ,点D是BC的中点,点E在AC上,且DE⊥A1E.
,点D是BC的中点,点E在AC上,且DE⊥A1E.
第9题图
(1)求证:平面A1DE⊥平面ACC1A1;
(2)求直线AD和平面A1DE所成角的正弦值.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






