向量作为工具,在数学、物理以及实际生活中都有着广泛的应用.作为一种重要的数学工具,向量在复数、解析几何、立体几何等方面有着更加灵活、多样化的运用,也更好地显示了数形结合的优势.

方法简述

1.化归思想

例1 已知a>0,函数的最小值为_________.

点拨 可引入向量坐标,利用向量的模解题.

解答 设,由,得a,则所求最小值为10a.

反思 本题利用化归思想将从函数的最值问题转化为主要考查向量的模的应用问题.

2.数形结合

例2 已知四边形ABCD的对角线AC⊥BD,且AC与BD互相平分.求证:四边形ABCD为菱形.

点拨 建立坐标系,数形结合.

证明:设AC交BD于O,以AC为x轴,BD为y轴,建立如图所示的平面直角坐标系.

例2答图

∵AC与BD互相平分,∴设C(a,0),A(-a,0),B(0,-b),D(0,b).

∴=(-a,b),=(-a,b),∴

∵A不在CD上,∴四边形ABCD为平行四边形.

又,且,∴

∴四边形ABCD为菱形.

反思 数形结合是解决向量问题的常用思想.

3.数学建模

例3 如图所示,直线EF,MN的交点是O,夹角是.一开始,甲在OE上距O点2千米的A处;乙在OM上距O点1千米的B处.现在他们同时以2千米/时的速度行走.甲沿EF的方向,乙沿NM的方向.设与OE同向的单位向量为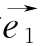,与OM同向的单位向量为.

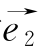例3图

(1)求

(2)若过2小时后,甲到达C点,乙到达D点,请用表示

(3)若过t小时后,甲到达G点,乙到达H点,请用表示

(4)什么时间两人间距最短?

点拨 本题可以从向量的分解定理出发进行研究,结合向量的加、减法以及向量的模的概念来进行求解.(www.daowen.com)

解答 (1)

(2)

(3),得

(4),当t=时,最小.

反思 通过向量的模的概念,将第(4)题转化为函数的最值问题进行研究.

例4 平面上三个非零向量两两夹角相等,,则等于______.

解答 ①若两两夹角为0°,则

②若两两夹角为120°,则×(1×3+3×7+1×7)=28,故填11或

易错分析 容易遗漏向量夹角为0的情况.

例5 设O(0,0),A(1,0),B(0,1),点P是线段AB上的一个动点,,若,则实数λ的取值范围是(　).

A.≤λ≤1　B.

C.　D.

解答

解得.因点P是线段AB上的一个动点,所以0≤λ≤1,即满足条件的实数λ的取值范围是.故选B.

易错分析 容易忽视“P在线段AB上”的情况对结果的影响.

1.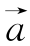=“向东走8千米”,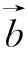=“向北走8千米”,则=_________

经典训练的方向是_________.

2.大小相等的三个力作用于同一点,欲使其合力为零,每两个力之间的角度大小均应为_________________.

3.有一两岸平行的河流,水流速为1,速度为的小船要从河的一边行驶向对岸,为使所行驶的路程最短,小船应朝______方向行驶.

4.已知三个力,某物体在这三个力的同时作用下保持平衡,则=(　).

A.(-1,8)　B.(1,-8)　C.(8,-1)　D.(-8,-1)

5.直角坐标系xOy中,分别是与x,y轴正方向同向的单位向量.在Rt△ABC中,若,则k的可能值个数是(　).

A.1　B.2　C.3　D.4

6.一个质点O受两个力的作用.已知牛,方向正东.另一力牛,方向北偏西30°.试求质点O受到的合力的大小,以及在合力作用下的运动方向(精确到0.01°).

7.已知平面内的四边形ABCD和点O,且求证:四边形ABCD为平行四边形.