两个向量![]() 的数量积是其中一个向量
的数量积是其中一个向量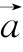 的模
的模![]() 与另一个向量
与另一个向量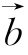 在向量
在向量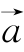 的方向上的投影
的方向上的投影![]() 的乘积.
的乘积.
对于用坐标表示的向量![]() ,它们的数量积是
,它们的数量积是![]()
方法简述
1.化归思想
化归不仅是一种重要的解题思想,也是一种最基本的思维策略,更是一种有效的数学思维方式.所谓的化归思想方法,就是在研究和解决有关数学问题时采用某种手段将问题通过变换使之转化,进而达到解决问题的一种方法.一般总是将复杂问题通过变换转化为简单问题;将难解的问题通过变换转化为容易求解的问题;将未解决的问题通过变换转化为已解决的问题.
例1图
例1 如图所示,在△ABC中,AD⊥AB,![]()
![]() ,则
,则![]() =________.
=________.
点拨 可利用向量的数量积公式进行转化.
解答
反思 本题主要考查平面向量、解三角形等基础知识,考查化归与转化的数学思想.
2.运用定义
例2 在边长为2的正△ABC中,设![]() ,求
,求![]()
点拨 要准确理解![]() 的夹角.
的夹角.
解答 ∵![]() 的夹角为120°,∴
的夹角为120°,∴![]() =2×2×cos120°=-2.
=2×2×cos120°=-2.
同理![]() ,即
,即![]()
反思 求向量的夹角时,应当先通过平移将向量![]() 的始点重合.
的始点重合.
3.方程思想
例3 已知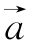 =(-1,-3),
=(-1,-3),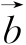 =(2,-5),且
=(2,-5),且![]() ,求:
,求:
(1)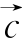 ;(2)
;(2) 与
与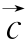 的夹角θ.
的夹角θ.
点拨 先设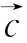 的坐标.
的坐标.
解答 (1)设![]() ,由
,由![]() ,得
,得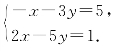
∴ ∴
∴![]() =(-2,-1).
=(-2,-1).
(2)cosθ=![]() .
.
反思 向量数量积的坐标表示比定义在形式上简单,计算上方便,因此在向量的计算中尽量使用向量的坐标.
4.等价转化
例4 若向量 =(cosα,sinα),
=(cosα,sinα),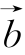 =(cosβ,sinβ),且
=(cosβ,sinβ),且![]()
点拨 可以将![]() 进行平方.
进行平方.
解答 (1)∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]()
(2)∵k+![]() ≥2或k+
≥2或k+![]() ≤-2,∴
≤-2,∴![]() (https://www.daowen.com)
(https://www.daowen.com)
又![]() ,∴
,∴![]()
∴![]()
反思 对于模的等式除了运用坐标代入之外,运用![]() 化简等式也是一种方法.
化简等式也是一种方法.
易错解读
例5 给定正整数n和正数M,对于满足条件![]() 的所有等差数列a1,a2,a3,…
的所有等差数列a1,a2,a3,…
试求S=an+1+an+2+…+a2n+1的最大值.
解答 设公差为d,则由题意,![]()
即![]() ,也就是
,也就是![]()
设![]() 得,
得,
当且仅当![]() 时,等号成立.
时,等号成立.
解得![]() ,所以S的最大值是
,所以S的最大值是![]()
易错分析 找不到本题的切入点.
经典训练
1.若向量![]() 满足
满足![]() ,
,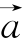 与
与 的夹角为120°,则
的夹角为120°,则![]() = ___________.
= ___________.
2.若![]() ,
,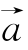 与
与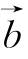 的夹角为钝角,则λ的取值范围是______.
的夹角为钝角,则λ的取值范围是______.
3.若向量![]() 满足
满足![]() ,则向量
,则向量![]() 的夹角的大小为________.
的夹角的大小为________.
4.![]() 均为非零向量,则
均为非零向量,则![]() 是
是![]() 的( ).
的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.设![]() 在
在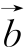 上的投影为
上的投影为![]() 在x轴上的投影为2,且
在x轴上的投影为2,且![]() ,则
,则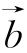 为( ).
为( ).
A.(2,14) B.![]() C.
C.![]() D.(2,8).
D.(2,8).
6.设O是直角坐标系的原点,![]() ,在x轴上求点P,使
,在x轴上求点P,使![]() 最小,并求此时的∠APB(用反三角函数表示).
最小,并求此时的∠APB(用反三角函数表示).
7.在△ABC中,
(1)若![]() ,求证:△ABC的面积
,求证:△ABC的面积![]()
(2)若![]() ,求证:△ABC的面积
,求证:△ABC的面积![]()
8.已知x∈R,向量![]()
(1)求函数f(x)解析式,并求当a>0时,f(x)的单调递增区间;
(2)当![]() 时,f(x)的最大值为5,求a的值.
时,f(x)的最大值为5,求a的值.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






