如果![]() 是同一平面内的两个不平行向量,那么对于这一平面内的任意向量a,有且仅有一对实数λ1,λ2,使
是同一平面内的两个不平行向量,那么对于这一平面内的任意向量a,有且仅有一对实数λ1,λ2,使![]()
方法简述
1.利用定义
例1图
例1 如图所示,不平行的三个向量![]() 有公共起点O,且满足
有公共起点O,且满足![]()
![]()
求证:![]() 三个向量的终点在一条直线上的充要条件是λ+μ=1.
三个向量的终点在一条直线上的充要条件是λ+μ=1.
证明 ①充分性:
所以![]() 三个向量的终点A,B,C三点在一条直线上.
三个向量的终点A,B,C三点在一条直线上.
②必要性:
若![]() 三个向量的终点A,B,C三点在一条直线上,则
三个向量的终点A,B,C三点在一条直线上,则![]()
即![]()
∴![]() ,则λ+μ=1.
,则λ+μ=1.
综上所述![]() 三个向量的终点在一条直线上的充要条件是λ+μ=1.
三个向量的终点在一条直线上的充要条件是λ+μ=1.
反思 在必要性证明中,![]() ,又
,又![]() ,而得到
,而得到![]() ,这是因为
,这是因为![]() ,且
,且![]() 是两个不平行的向量,由平面向量分解定理的唯一性,系数分别相等得到
是两个不平行的向量,由平面向量分解定理的唯一性,系数分别相等得到![]()
2.数形结合
例2图
例2 如图所示,设P,Q为△ABC内的两点,且![]()
![]() ,则△ABP的面积与△ABQ的面积之比为( ).
,则△ABP的面积与△ABQ的面积之比为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
点拨 可以从向量加法的几何意义的应用出发进行研究.
例2答图
解答 如图所示,设![]() ,则
,则![]()
![]() .由平行四边形法则可知,NP∥AB,所以
.由平行四边形法则可知,NP∥AB,所以![]()
![]() ,同理可得
,同理可得![]() .故选B.
.故选B.
反思 可利用向量的加法的平行四边形法则进行转化.
3.方程思想
例3图
例3 如图所示,点C在以O为圆心的圆弧![]() 上变动,且∠AOB=120°.若
上变动,且∠AOB=120°.若![]() ,其中x,y∈R,则x+y的最大值是______.
,其中x,y∈R,则x+y的最大值是______.
点拨 可利用向量数量积建立方程组解题.
解答 设∠AOC=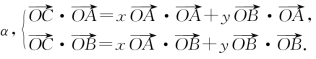
即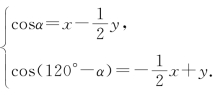
∴x+y=2[cosα+cos(120°-α)]=![]() ,即x+y的最大值是2.
,即x+y的最大值是2.
反思 本题主要考查向量数量积的运用,从而建立方程组,通过解方程组解决问题.
4.归纳法(www.daowen.com)
例4 已知直线y=3-x上两个点A(0,3),C(3,0).
(1)若![]() ,试确定D点与直线y=3-x的位置关系.
,试确定D点与直线y=3-x的位置关系.
(2)已知点B(1,2)是直线y=3-x上的一点,是否存在实数m,n使向量![]()
![]() ,如果存在,请求出m+n的值;如果不存在,则请说明理由.
,如果存在,请求出m+n的值;如果不存在,则请说明理由.
(3)研究(1)(2)问题的条件与结论,请提出一个更一般的命题,并研究该命题是否为真命题.
点拨 利用向量相等的概念求解(1)和(2),并在这两个结果的基础上进行归纳,从而研究(3).
解答 (1)D(4,-1),在直线y=3-x上.
(2)由(1,2)=(0,3m)+(3n,0)得![]()
(3)平面上A,B,C三点共线,及直线外一点O,![]() 的充要条件是m+n=1,为真命题.
的充要条件是m+n=1,为真命题.
反思 本题要用到两向量相等的坐标要求,即横、纵坐标均相等.(1)(2)两题结论的正确性决定了(3)归纳的结论是否正确.
易错解读
例5图
例5 如图所示,OM∥AB,点P在由射线OM、线段OB及AB的延长线围成的阴影区域内(不含边界)运动,且![]() 时,y的取值范围是________.
时,y的取值范围是________.
例5答图
解答 如图所示,过点P分别作OB,OA的平行线,分别交直线OA,OB于点E,F.
∴![]() .∵x=
.∵x=![]() ,∴OE=
,∴OE=![]() .由题可知P点在线段MN上移动,则F点介于F1,F2之间.由三角形相似可得F1处
.由题可知P点在线段MN上移动,则F点介于F1,F2之间.由三角形相似可得F1处![]() ,F2处
,F2处![]() ,所以
,所以![]()
易错分析 根据范围确定系数y时要熟悉相似三角形的比的关系.
经典训练
1.在△ABC中,已知D是AB边上一点,若![]() ,则λ=________.
,则λ=________.
2.已知O是△ABC所在平面内一点,D为BC边的中点,且![]()
![]() ,那么k=________.
,那么k=________.
第3题图
3.如图所示,平面内有三个向量![]() ,其中
,其中![]() 的夹角为120°
的夹角为120°![]() 的夹角为30°,且
的夹角为30°,且![]()
![]() ,若
,若![]() ,则λ+μ的值为________.
,则λ+μ的值为________.
第4题图
4.如图所示,平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ,Ⅱ,Ⅲ,Ⅳ(不包括边界).若![]() ,且点P落在第Ⅲ部分,则实数a,b满足( ).
,且点P落在第Ⅲ部分,则实数a,b满足( ).
A.a>0,b>0 B.a>0,b<0
C.a<0,b>0 D.a<0,b<0
5.在平面直角坐标系中,O为坐标原点,设向量![]() ,其中
,其中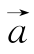 =(3,1),
=(3,1),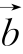 =(1,3).若
=(1,3).若![]() ,且0≤λ≤μ≤1,C点所有可能的位置区域用阴影表示正确的是( ).
,且0≤λ≤μ≤1,C点所有可能的位置区域用阴影表示正确的是( ).
6.已知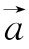 =(-1,2),
=(-1,2),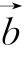 =(1,-1),
=(1,-1),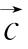 =(3,-2),且
=(3,-2),且![]() ,求实数p,q的值.
,求实数p,q的值.
7.已知![]() 是不共线的向量,若向量
是不共线的向量,若向量![]() 共线,求实数k的值.
共线,求实数k的值.
8.已知![]() 是不共线的向量
是不共线的向量![]() ,试用
,试用![]() 表示
表示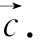 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






