向量是沟通代数、几何的一种工具.向量有非常直观的几何意义,是数与形的完美结合.一方面,它可以把几何问题转化为坐标的代数运算;另一方面,它还可以结合图形对向量的有关问题进行分析求解.
向量的坐标表示,即向量的代数表示.在引入向量的坐标表示后,可使向量运算代数化,将数与形紧密结合起来,这样几何问题的证明就可以转化为大家熟知的数量运算.
方法简述
1.方程思想
例1 已知集合![]() λ∈R},则M∩N=________.
λ∈R},则M∩N=________.
点拨 通过消去λ,得到向量的横、纵坐标之间的关系,继而利用方程思想进行求解.
解答 设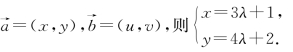
消λ,得4x-3y+2=0.①
同理,由N,得5u-4v+2=0.②
由①②,可得M∩N={(-2,-2)}.
反思 本题多次使用了方程的思想,通过消元得到方程,并利用方程组求解得到最后的结果.
2.等价转化
例2 将函数![]() 的图象沿向量
的图象沿向量![]() 的方向移动
的方向移动![]() 个单位得到函数
个单位得到函数![]() 的图象,求向量
的图象,求向量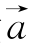 的坐标.
的坐标.
点拨 由于图象沿向量![]() 的方向移动
的方向移动![]() 个单位,则平移的方向及单位数就构成向量
个单位,则平移的方向及单位数就构成向量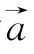 的坐标(m,n).
的坐标(m,n).
解答 ∵y=![]() 的图象经过向右平移
的图象经过向右平移![]() 单位,再向上平移1个单位,可得
单位,再向上平移1个单位,可得![]() 的图象,
的图象,![]()
反思 向量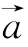 =(m,n)只提供了一个方向,平移的幅度与a的模有关.将向量问题等价转化为函数图象平移的问题是解决问题的关键.
=(m,n)只提供了一个方向,平移的幅度与a的模有关.将向量问题等价转化为函数图象平移的问题是解决问题的关键.
3.函数思想
函数思想体现了在解决数学问题中的一种思维策略.
具体来说,函数描述了自然界中数量之间的关系,函数思想通过提出问题的数学特征,建立函数关系型的数学模型,从而进行研究.它体现了“联系和变化”的辩证唯物主义观点.一般地,函数思想是构造函数(即“规定思想”)从而利用函数的性质(已知+未知+规定思想)解题.
在解题中,善于挖掘题目中的隐含条件,构造出函数解析式和妙用函数的性质,是应用函数思想的关键.对所给的问题观察、分析、判断比较深入、充分、全面时,才能产生由此及彼的联系,构造出函数原型.
例3 已知![]() ,试求
,试求![]() 的最大值和最小值.
的最大值和最小值.
点拨 求![]() 的最大值和最小值可以先求
的最大值和最小值可以先求![]() 的表达式.
的表达式.
解答 ∵![]()
∴![]()
∴![]() 的最大值为3,最小值为1.
的最大值为3,最小值为1.
反思 求![]() 的最值问题一般先求模的表达式,转化成函数求最值.不过由于点B在单位圆上,A为定点,因此还可以用数形结合的方法解决此问题,读者不妨可以试一试.
的最值问题一般先求模的表达式,转化成函数求最值.不过由于点B在单位圆上,A为定点,因此还可以用数形结合的方法解决此问题,读者不妨可以试一试.
4.利用定义
例4 已知A,B,C三点坐标分别为(-1,0),(3,-1),(1,2)![]()
(1)求点E,F及向量![]() 的坐标;
的坐标;
(2)求证:![]()
点拨 运用定比分点公式求点E,F的坐标,即可解决后续问题.
解答 (1)设![]() (www.daowen.com)
(www.daowen.com)
∵![]() ∴
∴![]() ,∴
,∴![]()
同理![]() ,可得
,可得![]() ,即
,即![]()
(2)∵![]() ,∴
,∴![]() 方向相同.
方向相同.![]()
反思 求E,F的坐标可以运用定比分点公式,也可以设E,F的坐标代入![]() 计算.证明向量平行,要抓住向量平行的定义.
计算.证明向量平行,要抓住向量平行的定义.
易错解读
例5 已知在△ABC中,过重心G的直线交边AB于点P,交边AC于点Q,设△APQ的面积为S1,△ABC的面积为S2,![]() ,求:
,求:
(1)![]()
(2)![]() 的取值范围.
的取值范围.
解答 设![]() .因为G是△ABC的重心,故
.因为G是△ABC的重心,故![]() ,因为
,因为![]() 与
与![]() 共线,所以
共线,所以![]() ,即
,即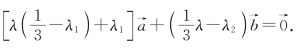 又
又![]() 不共线,所以
不共线,所以![]() ,消去λ,得λ1+λ2=3λ1λ2.
,消去λ,得λ1+λ2=3λ1λ2.
(1)![]() ,故
,故![]()
(2)![]() ,那么
,那么![]()
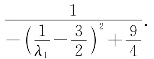 当P与B重合时,λ1=1;当P位于AB中点时,
当P与B重合时,λ1=1;当P位于AB中点时,![]() .故
.故![]() ,所以
,所以![]() .但因为P与B不能重合,故
.但因为P与B不能重合,故![]()
易错分析 注意本题的自变量的范围,因点P与点B不能重合,故λ1取不到1,所以![]() 取不到
取不到![]()
经典训练
1.已知a>0,若平面内三点A(1,-a),B(2,a2),C(3,a3)共线,则a=________.
2.已知向量![]() 且λ>0,则λ=________.
且λ>0,则λ=________.
3.已知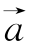 =(1,2),
=(1,2),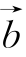 =(-3,2),当k= ________时
=(-3,2),当k= ________时![]() 平行.
平行.
4.下列命题中正确的个数是( ).
(1)若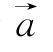 为单位向量,且
为单位向量,且![]() ,则
,则![]()
(2)若![]()
(3)若![]()
(4)若![]() ,则必有k=0(k∈R).
,则必有k=0(k∈R).
A.0 B.1 C.2 D.3
A.(-2,-4) B.(-3,-5) C.(3,5) D.(2,4)
6.经过点M(-2,3)的直线分别交x轴,y轴于A,B,且![]() ,求A,B的坐标.
,求A,B的坐标.
7.已知向量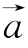 =(cosθ,sinθ)(θ∈[0,2π]),
=(cosθ,sinθ)(θ∈[0,2π]),![]() ,求:
,求:
(1)当θ为何值时,向量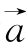 与
与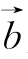 共线;
共线;
(2)![]() 的最大值和最小值.
的最大值和最小值.
8.如图所示,在平行四边形ABCD中,点E,F分别是AD,DC边的中点,BE,BF分别与AC交于R,T两点,你能发现AR,RT,TC之间有何关系吗?
第8题图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







