1.余弦定理
三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍,即a2=b2+c2-2bccosA,b2=a2+c2-2accosB,c2=a2+b2-2abcosC.
2.正弦定理
在一个三角形中,各边和它所对角的正弦之比相等,即![]()
3.解斜三角形
由斜三角形的六个元素(三条边和三个角)中的三个元素(至少有一个是边),求其余三个未知元素(可能有两解、一解或无解)的过程,叫作解斜三角形.
本节课利用正、余弦定理来解斜三角形.其解题思想、方法、规律、技巧如下所述.
方法简述
1.数形结合思想
它的主要特点:数⇒形⇒问题的解决或形⇒数⇒问题的解决.
事实上,数学作为客观事物的一种存在形式,其中任何问题都具备“形”的因素.从理论上说,任何一个数学问题都可发掘其中的“形”,并发挥它的直观作用,从而给出它的一些具有实体感的解答.几何中“形”的重要作用是不言而喻的,就代数的问题来说,若注意充分发挥“形”的作用,其效果往往比进行纯数学理论的抽象、烦琐甚至枯燥的推演要好得多.
例1 若![]() ,则S△ABC的最大值为________.
,则S△ABC的最大值为________.
点拨 数与形的结合,构造底边AB上高线的函数解析式,求出S△ABC的最大值.
解答 建立如图所示的直角坐标系,点B,A坐标分别为B(0,0),A(2,0),设点C坐标为C(x,y).
例1答图
由![]() ,得
,得![]()
化简,得![]() 其中,
其中,![]()
所以,当![]() 时,h(x)取最大值
时,h(x)取最大值![]()
所以△ABC的面积最大值为![]()
反思 本题求解方法与过程有多样性.
也可以设BC=a,则![]()
由余弦定理,得![]() ,则
,则![]()
那么![]() ,当且仅当a2=12,即
,当且仅当a2=12,即![]() 时,S△ABC取得最大值
时,S△ABC取得最大值![]()
2.三角形边角转换法
利用正弦定理和余弦定理等有关定理,将三角形的边、角相互转换以达到便利研究三角形有关问题的方法就是常用的边角转换法.
利用正弦定理将边转换为角,可以使原题中的代数与三角函数综合问题转化为纯三角比问题,便于利用三角公式进行变形,求得有关角的三角比关系或值.
利用正弦定理、余弦定理将角转换为边,又可以使三角比问题转化为代数问题,运用代数恒等变形得到边之间的关系,并为利用代数函数有关性质解决问题创造了有利条件.
在三角形中关于边、角的主要关系式有:
(1)A+B+C=180°;
(2)a+b>c,a-b<c(a,b,c对等地位,以下同);
(3)A>B⇔a>b;
(4)正弦定理![]()
(5)余弦定理:c2=a2+b2-2abcosC;
(6)a2+b2=c2⇔c为直角⇔cosC=0;
a2+b2<c⇔c为钝角⇔cosC<0;
a2+b2>c⇔c为锐角⇔cosC>0;
(7)sinA=sin(B+C);cosA=-cos(B+C);
(8)三角形面积公式:
例2 若△ABC满足a(bcosB-ccosC)=(b2-c2)cosA,试判断该三角形的形状.
点拨 由于该题条件是关于边或角的齐次式,可以采用两条思路证明:
(1)利用余弦定理,统一为边关系;
(2)利用正弦定理,统一为角关系.
解答 解法一:(统一为边关系)
由余弦定理,得![]()
即b2(a2+c2-b2)-c2(a2+b2-c2)=(b2-c2)(b2+c2-a2),
变形为2(b2-c2)(a2-c2-b2)=0,
所以b2=c2或a2=b2+c2,
即△ABC为等腰三角形或直角三角形.
解法二:(统一为角关系)
由正弦定理,得sinA(sinBcosB-sinCcosC)=(sin2B-sin2C)cosA,
故![]()
从而sinAcos(B+C)sin(B-C)=sin(B+C)sin(B-C)cosA,
于是sin(B-C)=0或sin(B+C-A)=0,
故B=C或B+C=A,
故△ABC为等腰三角形或直角三角形.
反思 一般地,我们可以利用正弦定理或余弦定理,将已知关系中的边转换为角,或角转换为边,然后从角或边的关系判断三角形的形状.
判断三角形形状常用如下方法(a,b,c表示边,A,B,C表示对应角):
(1)等边三角形:
①a=b=c;②sinA=sinB=sin60°;③A=B=C;④a=b,A,B,C中任一个为60°.
(2)等腰三角形:
①a=b;②sinA=sinB或cosA=cosB;③A=B;④cos(A-B)=1或sin(A-B)=0.
(3)直角三角形:
①a2+b2=c2;②cos![]() ;③sinA=1;④sin(A+B)=1;⑤cosA=0;⑥cos(A-B)=cosC(注意此时A或B为直角).
;③sinA=1;④sin(A+B)=1;⑤cosA=0;⑥cos(A-B)=cosC(注意此时A或B为直角).
(4)等腰或直角三角形:
sin2A=sin2B;
(5)等腰直角三角形:
①a=b,C=90°;②sinA=1,![]() ;③tanA=tanB=1.
;③tanA=tanB=1.
(6)钝角三角形:
①a2+b2<c2;②cosC<0;③tanC<0.
例3 已知△ABC的周长为![]() ,且
,且![]()
(1)求边AB的长;
(2)若△ABC的面积为![]() ,求C的大小.
,求C的大小.
点拨 面积公式以及正、余弦定理的综合应用.
解答 (1)由题意及正弦定理,得![]()
(2)由△ABC的面积为![]() ,得
,得![]()
由余弦定理,得![]()
所以C=60°.
反思 一般来讲,解三角形中边角关系问题有三条路:
①统一转化为边关系,利用代数方法研究;
②统一转化为角关系,利用三角函数恒等公式研究;
③灵活运用边、角关系,综合运用代数、三角公式研究.
例4 在△ABC中,已知三边a,b,c的对应角A,B,C满足![]()
(1)判断△ABC形状;
(2)若a=2,B=x,当x为何值时![]() 有最小值,并求该最小值.(www.daowen.com)
有最小值,并求该最小值.(www.daowen.com)
点拨 (1)化切为弦,再将三角比转化为B,C关系;
(2)利用换元法转化为代数函数,通过研究其单调性,求最值.
解答 (1)因为A+B+C=π,有sin(B+C)=sinA.
原式可化为![]()
所以2sinBsinC=cosBcosC+sinBsinC,
即cosBcosC-sinBsinC=cos(B+C)=0,解得![]()
故△ABC为直角三角形.
(2)在Rt△ABC中![]()
有b=2sinx,c=2cosx,
所以![]()
令![]() ,则
,则![]()
所以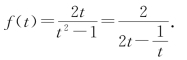
又由于![]() 在
在![]() 上单调递增,因此
上单调递增,因此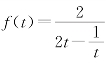 在
在![]() 上单调递减.
上单调递减.
由![]() ,得
,得![]()
仅当![]() 即
即![]() 时,等号成立.
时,等号成立.
故![]()
反思 令sinx+cosx=t,则![]() .这是一种有用的代换,可以把三角问题转化为代数问题,从而可利用函数方法处理问题.
.这是一种有用的代换,可以把三角问题转化为代数问题,从而可利用函数方法处理问题.
易错解读
例5 已知在△ABC中![]() .求cosC.
.求cosC.
解答 ∵0<A<π,![]()
又sinA>sinB,∴A>B.∴![]()
由![]() ,可得
,可得![]()
∴cosC=-cos(A+B)=-cosAcosB+![]()
易错分析 在解三角形时,三角形解的个数是一个很容易忽视的问题.
本题学生易犯下列错误:
由sinB=![]() ,∴0<B<π,∴cosB=
,∴0<B<π,∴cosB=![]() .
.
∴cosC=-cos(A+B)=-cosAcosB+sinAsinB=![]()
例6 在△ABC中,角A,B,C所对的边分别为a,b,c,且![]()
(1)求![]() 的值;
的值;
(2)若![]() ,求bc的最大值.
,求bc的最大值.
(2)∵![]()
∴![]() .又∵
.又∵![]()
当且仅当![]() 时
时![]() ,故bc的最大值是
,故bc的最大值是![]()
易错分析 解斜三角形中求三角形一边长或求三角形面积可用正弦定理、余弦定理来处理,除记清两定理内容外,两公式易用错.
经典训练
1.在△ABC中,若![]() ,C=150°,BC=1,则AB= ________.
,C=150°,BC=1,则AB= ________.
2.在△ABC中,三个角A,B,C的对边边长分别为a=3,b=4,c=6,则bccosA+cacosB+abcosC的值为________.
3.在△ABC中,AB=5,AC=3,BC=7,则∠BAC的大小为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.设锐角△ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA.
(1)求B的大小;
(2)求cosA+sinC的取值范围.
5.甲船以每小时![]() 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距![]() 海里,问乙船每小时航行多少海里?(1海里=1.852千米)
海里,问乙船每小时航行多少海里?(1海里=1.852千米)
6.在△ABC中,a,b,c分别是三个内角A,B,C的对边.若![]() ,求△ABC的面积.
,求△ABC的面积.
7.如图所示,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2.
第7题图
(1)求cos∠CBE的值;
(2)求AE.
8.已知△ABC的外接圆的半径为![]() ,内角A,B,C的对边分别为a,b,c,向量
,内角A,B,C的对边分别为a,b,c,向量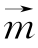 =(sinA
=(sinA![]() ,且
,且![]()
(1)求角C;
(2)求△ABC的面积S的最大值.
9.在△ABC中,若a=2bcosC,则△ABC是( ).
A.等腰三角形 B.等腰直角三角形
C.直角三角形 D.等腰或直角三角形
10.若A为△ABC的内角,则下列函数中一定取正值的是( ).
A.sinA B.cosA C.tanA D.![]()
11.在△ABC中,角A,B均为锐角,且cosA>sinB,则△ABC的形状是( ).
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等腰三角形
12.等腰三角形一腰上的高是![]() ,这条高与底边的夹角为60°,则底边长为( ).
,这条高与底边的夹角为60°,则底边长为( ).
A.2 B.![]() C.3 D.
C.3 D.![]()
13.在△ABC中,若b=2asinB,则A等于( ).
A.30°或60° B.45°或60° C.120°或60° D.30°或150°
14.在Rt△ABC中,C=90°,则sinAsinB的最大值是_________.
15.在△ABC中,∠A=60°,b=1,![]() ,则
,则![]() =_________.
=_________.
16.若A,B是锐角三角形的两个内角,则tanAtanB_________1(填“>”或“<”).
17.在△ABC中,若a=9,b=10,c=12,则△ABC的形状是________.
18.在△ABC中,若![]() ,则A=________.
,则A=________.
19.某观察站C在A城的南偏西20°方向,由A城出发有一条公路,走向是南偏东40°,距C处31千米的公路上的B处有一人正沿公路向A城走去,走了20千米后到达D处,此时CD距离为21千米,问这个人还需走多少千米才能到达A城?
20.在△ABC中,若(a+b+c)(a-b+c)=3ac,且tanA+tanC=3+![]() ,AB边上的高为
,AB边上的高为![]() ,求角A,B,C的大小与边a,b,c的长.
,求角A,B,C的大小与边a,b,c的长.
21.如图所示,在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30米,至点C处测得顶端A的仰角为2θ,再继续前进![]() 米至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高.
米至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高.
第21题图
22.在△ABC中,最大角A为最小角C的2倍,且三边a,b,c为三个连续整数,求a,b,c的值.
23.如图所示,有两条相交成60°角的直路EF,MN,交点是O.起初,阿福在OE上距O点3千米的点A处;阿田在OM上距O点1千米的点B处.现在他们同时以4千米/时的速度行走,阿福沿EF的方向行走,阿田沿NM的方向行走.
(1)求起初两人的距离;
第23题图
(2)用包含t的式子表示t小时后两人的距离;
(3)什么时候他们两人的距离最短?
24.某城市有一条公路,自西向东经过A点到市中心O点后转向东北方向OB,现要修建一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10千米,问把A,B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.(不要求作近似计算)
25.已知A,B,C是△ABC的三个内角![]()
(1)若任意交换两个角的位置,y的值是否变化?试证明你的结论.
(2)求y的最小值.
26.在△ABC中![]() ,判断这个三角形的形状.
,判断这个三角形的形状.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







