在物理和工程技术的许多问题中,经常要遇到形如y=Asin(ωx+φ)的函数(其中A,ω,φ都是常数).例如,物体简谐振动时位移与时间t的关系、交流电中电流I与时间t的关系等,都可以由这类函数解析式表示.

方法简述

1.转化化归思想

例1 已知函数f(x)=(sinx-cosx)sinx+(3cosx-sinx)cosx(x∈R).

(1)求函数f(x)的周期;

(2)函数f(x)的图象是由函数的图象经过怎样的变换得到的?

点拨 就像考虑三角函数的其他性质一样,把三角函数式化作只含一个三角符号的一次式是求解此类题的决定性步骤,然后套用正弦(或余弦、正切、余切)型函数y=Asin(ωx+φ)+k的最小正周期公式即可.另外,三角函数的图象变换是重点也是难点,要求学生切实掌握平移和伸缩变换的规律.

解答 f(x)=sin2x+3cos2x-2sinxcosx=2-sin2x+cos2x=

(1)函数f(x)的最小正周期为π.

(2)函数的图象向左平移个单位得到函数的图象;将函数的图象向上平移2个单位得到函数的图象,即将函数的图象按向量平移得到函数f(x)的图象.

反思 三角函数的图象和性质在本章中占有非常重要的地位,因此,必须认真掌握三角函数的图象特征,图象变换(平移、伸缩)理论,以及三角函数的定义域、值域、单调性、奇偶性、周期性、对称性等性质,并能以三角变换为手段,以其中的数学思想和方法为依托解决三角函数与向量、函数的综合问题.

例2图

例2 已知电流I与时间t的关系式为I=Asin(ωt+φ).

(1)如图是在一个周期内的图象,根据图中数据求I=Asin(ωt+φ)的解析式;

(2)如果t在任意一段秒的时间内,电流I=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?

点拨 本题主要考查三角函数的图象与性质等基础知识,考查运算能力和逻辑推理能力.

解答 (1)由图可知A=300.

设

则周期

∴

又当时,I=0,即

而

故所求的解析式为

(2)依题意,周期

∴ω≥300π>942.又ω∈N,故最小正整数ω=943.

反思 本题解答的关键点是将图形语言转化为符号语言,其中读图、识图、用图是数形结合的有效途径.

例3 设函数,给出以下四个论断:

①它的最小正周期为π;

②它的图象关于直线成轴对称图形;

③它的图象关于点成中心对称图形;

④在区间上是增函数.

以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题_________(用序号表示即可).

点拨 本题是一个开放性题目,综合考查了正弦型函数的单调性、周期性以及对称性.

解答 若①②成立,则,k∈Z,且,故k=0,∴φ=.此时,∴f(x)的图象关于成中心对称;又f(x)在上是增函数,∴在上也是增函数,因此可得①②⇒③④.用类似的分析可得①③⇒②④.因此填①②⇒③④或①③⇒②④.

反思 三角函数的周期性、对称性是三角函数的特有性质,要切实掌握,并注意结合三角函数的图象,从而达到解决问题的目的.

2.函数与方程思想

例4 若函数的最大值为2,试确定常数a的值.

点拨 三角函数的最值问题是一个常考知识点,要求学生切实掌握三角函数的值域,并且能熟练地对所给三角函数进行变形,转化为正、余弦函数,从而利用正、余弦函数的有界性求出所给函数的最值.

解答 f(x)=,其中,,解得

反思 三角函数最值类型常有两种解法:一是化为只含一个三角符号的一次式后利用正弦或余弦函数的有界性,要特别注意自变量的范围限制;二是通过换元转化为有范围限制的一元二次函数的最值问题.

3.数形结合思想

例5 方程在(0,2π)上有两个不同根α,β,求m的范围及α+β的值.

点拨 本题如果直接去考虑方程的根的情况,比较困难.遇到这种情况的时候,我们不妨换个角度来看问题.正所谓“退一步海阔天空”“横看成岭侧成峰”.当我们把方程的左右两边分开来看时,思路就有了.这可以用数形结合的方法解决.

解答 原方程即

例5答图

两函数的图象如图所示.由图知,当时,

原方程在(0,2π)总有两个不同根.另一方面,

当时,α,β关于对称,故,所以

当时,α,β关于对称,故,所以

反思 数形结合是一种非常重要的数学思想方法.在求解数学问题中,如果能充分地结合图形,往往能达到意想不到的效果.三角函数是函数的一种,所以有关函数中的数形结合,都可移植到三角函数中来:如方程根的个数的探讨、解不等式、求单调性与值域等,只要看作函数时,图象易于作出即可.

4.分类讨论思想

例6 是否存在实数a,使得函数在闭区间上的最大值是1?若存在,求出对应的a值;若不存在,试说明理由.

点拨 转化成二次函数问题.

解答

当时,0≤cosx≤1.

若,即a>2,则当cosx=1时,,所以(舍去);

若,即0≤a≤2,则当时,所以或a=-4<0(舍去);

若,即a<0,则当cosx=0时,所以(舍去);

综上所述知,存在符合题设.

反思 注意二次函数的定义域.

5.辅助角法

例7 设0<x<π,则函数的最小值是(　).

A.3　B.2　C.　D.

点拨 可以将y暂时看作参数,引入辅助角,利用三角函数的有界性去解.

解答 解法一:因为ysinx+cosx=2,所以

由|sin(x+φ)|≤1得,所以y2≥3.

又0<x<π,所以y>0.

又当时,解得

即当时,故选C.

解法二:由得ysinx=2-cosx.

两边平方整理,得(y2+1)cos2x-4cosx+4-y2=0.

令cos=t,将上式可看成代数方程(y2+1)t2-4t+4-y2=0.

于是Δ=16-4(y2+1)(4-y2)=4y2(y2-3)≥0.

又0<x<π,有y>0,所以,仅当时,等号成立,故

反思 辅助角法是利用asinx+bcosx=c转化为,将一个含正、余弦一次式的式子化为仅含一个函数(正弦)的式子,便于利用正弦函数的性质(如有界性)解决问题.该题的解法很多,还可以通过换元等手段转化为代数函数后利用求最值的方法求解.

6.三角图象变换法

将正弦函数y=sinx图象按照函数初等变换的法则变成为函数y=Asin(ωx+φ)的图象以解决有关问题的方法,就是三角函数y=Asin(ωx+φ)图象变换法.

函数y=sinx图象的初等变换有:

(1)对称变换

y=sinx→y=sin(-x),作y=sinx关于y轴对称图象而得;

y=sinx→y=-sinx,作y=sinx关于x轴对称图象而得.

(2)平移变换

y==sin(x+a),将y=sinx沿x轴方向平移|a|个单位而得;

y==sinx+b,将y=sinx沿y轴方向 平移|b|个单位而得.

(3)伸缩变换

y==sinωx(ω>0且ω≠1),将y=sinx图象上所有点的横坐标伸长(0<ω<1)或缩短(ω>1)到原来的(纵坐标不变)而得;

y==Asinx(A>0且A≠1),将y=sinx图象上所有点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍(横坐标不变)而得.

要得到函数y=Asin(ωx+φ)+b图象一般有=24条途径,但无论哪条途径,对于每种变换都是对变量x(或y)进行的.(www.daowen.com)

例8 要得到函数y=sinx的图象,只需将函数的图象(　).

A.向右平移个单位　B.向右平移个单位

C.向左平移个单位　D.向左平移个单位

点拨 利用三角函数变换方法中的相位变换进行解题,但是要注意相应的两个三角函数不是同一类型.

解答 y=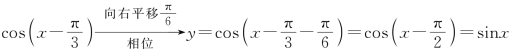,故选A.

反思 在三角函数的相位变换中,,将y=sinx沿x轴方向平移|a|个单位而得,通俗地说是“左加,右减;上加,下减”,并且在解题时一定要注意函数中的三角符号是否统一,细心很重要.

例9 将函数的图象按向量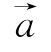平移后所得的图象关于点中心对称,则向量的坐标可能为(　).

A.　B.　C.　D.

点拨 这是三角函数图象变换、对称性与向量知识结合的题目,也是近年的高考中常常出现的题型.向量的坐标即为三角函数平移的依据.

解答 设=(h,0),则平移后所得的函数为,图象关于点对称,从而有(其中k∈Z),故选C.

反思 设向量

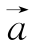=(h,0),则在三角函数平移中将,其中注意中ω=2,故应将x前的ω=2提出,在括号中减去h,千万不能直接在2x后面减去h.

函数图象变换的关键是正确掌握变换的规律,容易出错的地方是伸缩变换或平移变换的先后顺序不同,平移量也不同.一般地,当横向变换时,若先平移后伸缩,则平移|φ|个单位;若先伸缩后平移,则平移个单位.当纵向变换时,若先平移后伸缩,则平移个单位;若先伸缩后平移,则平移|b|个单位.

易错解读

例10 设关于x的函数y=2cos2x-2acosx-(2a+1)的最小值为f(a),试确定满足的a值,并对此时的a值求y的最大值.

点拨 本题主要考查最值问题、三角函数的有界性、计算能力以及较强的逻辑思维能力,知识点的依托是二次函数在给定区间上的最值问题.

解答 由及cosx∈[-1,1],得

因为,所以

故,解得a=-1.

所以.当cosx=1,即x=2kπ(k∈Z)时,ymax=5.

易错分析 对区间的分类易出错.利用等价转化把问题化归为二次函数问题,还要用到配方法、数形结合、分类讨论等.

例11 已知函数

(1)求函数f(x)的最小正周期;

(2)求f(x)的最小值及取得最小值时相应的x的值;

(3)若当时,f(x)的反函数为f-1(x),求f-1(1)的值.

解答

∴f(x)的最小正周期T=π.

(2)当时,f(x)取得最小值-2.

(3)令

∴

则,故

易错分析 学生在求f-1(1)的值时易走弯路.

本难点所涉及的问题以及解决的方法主要如下:

(1)求值问题的基本类型:①给角求值;②给值求值;③给式求值;④求函数式的最值或值域;⑤化简求值.

(2)技巧与方法:

①要寻求角与角关系的特殊性,化非特殊角为特殊角,熟练准确地应用公式.

②注意切割化弦、异角化同角、异名化同名、角的变换等常规技巧的运用.

③对于条件求值问题,要认真寻找条件和结论的关系,寻找解题的突破口,很难入手的问题,可利用分析法.

④求最值问题,常用配方法、换元法来解决.

经典训练

1.已知函数,则下列判断正确的是(　).

A.此函数的最小正周期为2π,其图象的一个对称中心是

B.此函数的最小正周期为π,其图象的一个对称中心是

C.此函数的最小正周期为2π,其图象的一个对称中心是

D.此函数的最小正周期为π,其图象的一个对称中心是

2.已知函数y=tanωx在内是减函数,则(　).

A.0<ω≤1　B.-1≤ω<0　C.ω≥1　D.ω≤-1

3.函数f(x)=Asin(ωx+φ)+b的图象如图所示,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2006)的值分别为(　).

A.f(x)=+1,S=2006

第3题图

B.

C.

D.

4.已知函数y=2sinωx在上单调递增,则实数ω的取值范围是(　).

A.　B.(0,2]　C.(0,1]　D.

5.要得到函数的图象,只需把函数的图象(　).

A.向左平移个单位　B.向右平移个单位

C.向左平移个单位　D.向右平移个单位

6.将的图象上所有的点的横坐标扩大到原来的2倍(纵坐标不变),得到y=g(x)的图象,再将y=g(x)的图象按向量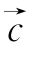平移,得到y=cosx的图象,则=(　).

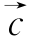A.　B.　C.　D.

7.定义运算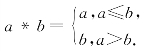例如1*2=1,则函数f(x)=sinx*cosx的值域为________.

8.已知P(1,cosx),Q(cosx,1),x∈

(1)求向量的夹角θ的余弦用x表示的函数f(x);

(2)求cosθ的最值.

9.已知(a∈R,a为常数).

(1)若x∈R,求f(x)的最小正周期;

(2)若f(x)在上最大值与最小值之和为5,求a的值;

(3)在(2)条件下f(x)先按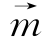平移后再经过伸缩变换后得到y=sinx,求.

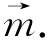10.如图所示,某地一天从6时至14时的气温变化曲线近似满足函数y=Asin(ωx+φ)+b.

第10题图

(1)求这段时间的最大温差;

(2)写出这段曲线的函数解析式.

11.设实数x,y,m,n满足m2+n2=a,x2+y2=b(a,b是正常数,且a≠b),那么mx+ny的最大值是(　).

A.　B.　C.　D.

第12题图

12.已知f(x)是定义在(0,3)上的函数,图象如图所示,那么不等式f(x)cosx<0的解集是(　).

A.(0,1)∪(2,3)　B.

C.　D.(0,1)∪(1,3)

13.函数与函数y=2的图象围成一个封闭图形,这个封闭图形的面积是________.

14.设x=f(θ)=(sinθ-2)2+1,则y=g(x)=x2-6x+6的最大值是________,最小值是________.

15.求函数的最大值和最小值.

16.如图所示,某海滨浴场的岸边可近似地看作直线a,救生员现在岸边的A处,发现海中的B处有人求救,救生员没有直接从A处游向B处,而是沿岸边从A处跑到离B处最近的D处,然后游向B处,若救生员在岸边的行进速度为6米/秒,在海水中的行进速度为2米/秒.

(1)分析救生员的选择是否正确;

(2)在AD上找一处C,使救生员从A到B的时间最短,并求出最短时间.

第16题图

17.已知函数的定义域为,值域为[-5,1],求a和b的值.