在物质世界里存在着许多周期性的现象,在物理学中也常常研究周期性运动.正弦函数和余弦函数就是描述周期性运动的数学模型,它产生于测量、航海和天文学,还在机械制造、电工学等学科中有着广泛的应用.在本节课中我们将研究正弦函数与余弦函数的图象与性质.

1.y=sinx,x∈R(图(a))和y=cosx,x∈R(图(b))的图象,分别叫作正弦曲线和余弦曲线.

2.用五点法作正弦函数和余弦函数的简图(描点法).

余弦函数y=cosx,x∈[0,2π]的五个关键点是

3.图象和性质图表解.

方法简述

1.数形结合思想

数形结合思想是高考中必考的数学知识,在三角函数中有非常明显的体现,并且运用到实处会有意想不到的效果.

例1 偶函数f(x)在上的解析式为y=sin2x,且是f(x)的图象的一条对称轴,则f(x)的最小正周期、最小值分别是(　).

点拨 能根据题设条件画出y=|sin2x|的图象,再由图象就能观察出f(x)的最小正周期和最小值.

例1答图

解答 依题意,y=|sin2x|的图象如图所示.

从图象上可以看出,故选C.

反思 本题考查函数性质,对称性,周期性,三角函数的最值问题以及数形结合能力.

2.五点法

正、余弦函数在一个周期内有五个关键点,即最高点、最低点以及图象与平衡位置的三个交点.先找出这五个关键点,再用光滑曲线联结起来,画出图象,通过图象来研究三角函数有关性质,这种依靠三角函数图象的直观性来解决有关问题的方法,叫作五点法.

用五点法作出正、余弦函数在一个周期内的简图,基本步骤如下:

(1)列表,找出五个特征点,起点、终点、零点、最大值点、最小值点;

(2)描点;

(3)作图,即用光滑的曲线联结.

用图象法解三角函数问题一般步骤如下:

(1)根据题意画出题设条件中有关三角函数的图象;

(2)将三角函数问题转化为对其函数图象的研究,分析图象的数量特征,找出图象中有关点、线互相关系;

(3)将图象中的位置关系和数量关系转化为相应的三角函数关系,从而使问题得到解决.

(1)求φ;

(2)求函数y=f(x)的单调递增区间;

点拨 易得因为此函数周期为,所以[0,π]是函数的一个周期区间,但是由于当;又当因此是一个完整的周期区间,但并不全部包括上面所说的五个关键点.因此必须将表作适当调整.

解答 (1)因为是函数y=f(x)图象的一条对称轴,有得

(2)f(x)=

因此函数y=f(x)的单调增区间为

3.利用有界性法

例3 a,b是不相等的正数,求的最大值和最小值.

点拨 将函数中的三角符号统一,再利用正余弦函数的值域,求此函数的最值.

解答 y是正值,故使y2达到最大(或最小)的x值也使y达到最大(或最小).

∵a≠b,(a-b)2>0,0≤sin22x≤1,

∴当sin2x=±1时,即时,y有最大值2(a+b);

当sin2x=0时,即时,y有最小值a+b.

反思 利用三角函数的有界性如|sinx|≤1,|cosx|≤1来求三角函数的最值.

易错解读

例4 求函数的单调增区间.

错解 令

∵y=sinu在上递增,∴

解得-4k≤x≤-4k+2.

∴原函数的单调递增区间为[-4k,-4k+2](k∈Z).

易错分析 上述解答貌似正确,实则错误,错误的原因是,令,忽略了u是x的减函数,未考虑函数复合后单调性的变化.

解答 解法一:令,则u是x的减函数.

又y=sinu是上的减函数,

∴原函数在上单调递增.

设

解得-4k-2≤x≤-4k(k∈Z).

∴原函数在[-4k-2,-4k](k∈Z)上单调递增.

∵为增函数,∴只需求sinu的递减区间.

∴,解得4k+2≤x≤4k+4(k∈Z).

∴原函数的单调递增区间为[4k+2,4k+4](k∈Z).(www.daowen.com)

例5 试判断下列各函数的奇偶性.

(1)f(x)=

(2)f(x)=

解答 (1)f(x)的定义域x∈R,因为

所以f(-x)=-f(x),则f(x)是奇函数.

(2)先考虑函数的定义域.

因为1+sinx+cosx≠0,所以

则且x≠2kπ-π(k∈Z).因此,定义域关于原点不对称,函数无奇偶性.

例如,令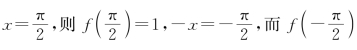无意义,因此f(-x)≠f(x),并且f(-x)≠-f(x),故f(x)是非奇非偶函数.

易错分析 研究函数性质之前应考虑函数的定义域.处理有关函数问题时,化简必须是等价变换,否则可能发生错误.

例如: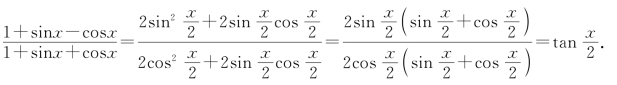

由于函数是奇函数从而得出原函数也是奇函数的错误结论.事实上,最后的约分破坏了变换的等价性的限制被取消是导致错误的根本原因.

经典训练

1.函数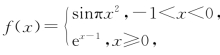若f(1)+f(a)=2,则a的所有可能值为(　).

A.1　B.1,　C.　D.

2.若函数f(x)=asinax+acosax(a>0)的最大值是,则函数f(x)的最小正周期是(　).

A.　B.　C.π　D.2π

3.已知函数,则f(1)+f(2)+f(3)+…+f(2003)=(　).

A.2003　B.　C.0　D.

5.已知函数的最大值为,最小值为,则a=_________,b=________.

6.(1)求函数的定义域;

(2)求函数的定义域.

7.已知函数f(x)=cos4x-2sinxcosx-sin4x.

(1)求f(x)的最小正周期;

(2)若,求f(x)的值域.

9.已知函数f(x)=-sin2x+sinx+a.

(1)当f(x)=0有实数解时,求实数a的取值范围;

10.化简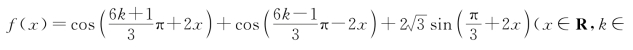Z),并求函数f(x)的值域和最小正周期.

11.函数f(x)=|sinx+cosx|的最小正周期是(　).

C.π　D.2π

12.函数的最小正周期是(　).

A.　B.π　C.2π　D.4π

A.[-1,1]　B.　C.[-2,2]　D.[-1,2]

14.若2α+β=π,则y=cosβ-6sinα的最大值和最小值分别是(　).

A.7,5　B.7,　C.5,　D.7,-5

15.设函数,若对任意x∈R都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为(　).

A.4　B.2　C.1　D.

16.函数y=cos2x+sinxcosx的最小正周期T=________.

17.函数的值域是________.

18.若sin2α+2sin2β=2cosα,求y=sin2α+sin2β的最大、最小值.

19.求函数f(x)=cos2x+2asinx-1(0≤x<2π,a∈R)的最值.

20.若cos2θ+2msinθ-2m-2<0对任意实数θ恒成立,试求实数m的取值范围.