二倍角的正弦、余弦、正切公式分别是：

sin2α=2sinαcosα,cos2α=cos2α-sin2α=1-2sin2α=2cos2α-1,

tan2α=.

方法简述

1.数形结合思想

点拨 构造出是本题的关键.

证明 在直角坐标系中,构造单位圆,如图所示.

设∠AOB=α,则,过点A作AD⊥x轴于D,

在Rt△ACB中,AD=sinα,CD=CO+OD=1+cosα,

所以

联结AB,则

在Rt△ADB中,

综上所述,

例1答图

反思 在锐角范围内,很多三角公式的推导都可以构造三角形或者单位圆,从图形中直观体现,若要进一步得到任意角的半角的正切公式,可以再利用诱导公式.

2.分类讨论思想

例2 已知的值.

点拨 先化简再求值.

解法一：由,所以有

所以

解法二：由于

所以

反思 三角公式必须非常熟练.

3.化归思想

将面临的数学新问题,通过消元、降次等方法和手段化归为已经解决了的问题,或是化归为熟悉的、简单的、特殊的、具体的问题,通过解决新问题而将原问题解决,这种解决问题的方法就是化归思想.

例3 试用sinα表示sin3α.

点拨 将角进行拆分.

反思 这个式子称为三倍角正弦公式,类似地,也可以通过化归思想推导出三倍角余弦、正切公式.

4.等价转化思想

点拨 本题方法较多,换元法转成二次函数问题,或参变量分离也可以.

解答 解法一：问题等价于sin2x-(a-4)(sinx+cosx)+a≥0恒成立.

设,则问题转化为f(t)的最小值大于或等于0即可.下面求函数f(t)的最小值.

f(t)可化为

①当时,函数f(t)在定义域内单调递增,,解得

又因为,所以a∈∅.

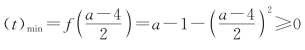②当时,函数f(t)在顶点处取得最小值,所以f,解得2≤a≤10.

综上所述,

解法二：问题等价于sin2x-(a-4)(sinx+cosx)+a≥0恒成立.

令t=sinx+cosx,则问题转化为恒成立.

将不等式t2-(a-4)t+a-1≥0看成关于a的一次不等式a(t-1)≤t2+4t-1.

①当t=1时,上述不等式为0≤4,恒成立,所以a∈R.

②当时,a(t-1)≤t2+4t-1恒成立,即为恒成立.

设,则问题转化为a≥g(t)max即可,当t=-1时,取到等号,所以g(t)max=2,所以a≥2.

③当时,a(t-1)≤t2+4t-1恒成立,即为恒成立.

设,则问题转化为a≤g(t)min即可,,函数g(t)在内单调递减,所以

综上所述,(www.daowen.com)

反思 此题考查的是换元法,转化思想,在换元时要注意变量的取值范围.

5.逆向倒推法

点拨 观察角的变化规律,连续逆用二倍角公式.

反思 在求值中,形如cosθcos2θcos22θ…cos2n-1θ的运算中,可将分母看作1,分子、分母同乘2nsinθ,然后分子不断地逆用倍角公式,则原式可化为,若2nθ=kπ±θ(k∈Z),即可求出原式的值为

易错解读

例6 函数是(　).

A.奇函数

B.偶函数

C.奇函数又是偶函数

D.非奇非偶函数

因为,所以f(x)为奇函数.故选A.

易错分析 没有考虑函数f(x)的定义域,忽视了一个函数f(x)为奇(偶)函数的必要条件,即定义域关于原点对称.

例7 已知,则cosxsiny的取值范围是(　).

A.　B.　C.　D.[-　1,1]

错解二 cosxsiny=t,则,即,故-t≤1,所以,故选C.

易错分析 上述两个解答的主要错误是没有注意在设cosxsiny=t时,这个t已经具有一个范围,若单独考虑,就会出现上述错误.

解答 A.设cosxsiny=t,则可得sin2xsin2y=2t.由

经典训练故选A.

1.已知且180°＜φ＜270°,求sin2φ,cos2φ,tan2φ的值.

2.若,求sin2θ的值.

3.2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形,如图所示.如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cos2θ的值等于_________.

第3题图

4.利用二倍角公式求下列各式的值.

(2)tan15°+cot15°.

5.已知,且α,β∈(0,π),求tan(2α-β)的值.

6.已知,求tanA的值.

7.设,求cos2α和的值.

9.化简：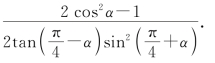

10.证明下列恒等式：

11.已知

(1)若x∈R,求f(x)的最小正周期;

(2)若f(x)在上的最大值与最小值之和为3,求a的值.

12.已知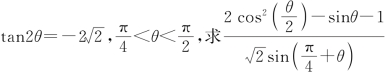的值.

13.已知F(θ)=cos2θ+cos2(θ+α)+cos2(θ+β),问是否存在满足0≤α＜β≤π的α,β,使得F(θ)的值不随θ的变化而变化？若存在,求出α,β;若不存在,说明理由.