1.同角三角比的关系

(1)倒数关系：tanα·cotα=1,cscα·sinα=1,secα·cosα=1.

(2)商数关系：

(3)平 方关系：sin2α+cos2α=1,sec2α=tan2α+1,csc2α=cot2α+1.

2.诱导公式(见下表)

记忆口诀是“奇变偶不变,符号看象限”.所谓“奇变偶不变”是指对,函数名变为它的余函数;对π±α,2π±α,则不变.所谓“符号看象限”是指把诱导公式中的任意角α看成锐角,然后观察角的终边所在象限内原函数的符号来确定符号.

方法简述

1.分类讨论思想

在研究与解决数学问题时,可根据数学对象的本质属性的相同和不同,确定同一划分标准,将数学对象区分为不同种类,然后逐类进行研究与求解,并综合得出答案,从而达到研究与解决问题的目的,也就是说：(1)对何种事物分类,即确定分类对象;(2)按什么要求分类,即选择分类的标准;(3)分成的种类,即确定分类的结果.这种思想就是分类讨论思想.

例1 化简：

(1)(n∈Z);(2).

点拨 分类讨论.

②当n=2k+1(k∈Z)时,原式=

①当n为奇数时,原式=

②当n为偶数时,原式=

综上所述,原式=0.

反思 注意诱导公式符号的变化特点.

2.等价转化思想

例2 已知sinα+cosα=,α∈(0,π),求sin3α+cos3α的值.

点拨 合理运用好sinα与cosα的关系.

解答 因为sin3α+cos3α=(sinα+cosα)(sin2α-sinαcosα+cos2α),(sinα+cosα)2=1+2sinαcosα,sinαcosα=,

所以sin3α+cos3α=

反思 注意角的范围的作用.

3.逆向倒推法

例3 求tan2Atan(30°-A)+tan2Atan(60°-A)+tan(30°-A)tan(60°-A)的值.

点拨 联想两角和差展开公式.

解答 原式=tan2A[tan(30°-A)+tan(60°-A)]+tan(30°-A)tan(60°-A)

=tan2Atan[(30°-A)+(60°-A)][1-tan(30°-A)tan(60°-A)]+ tan(30°-A)tan(60°-A)

=tan2Acot2A[1-tan(30°-A)tan(60°-A)]+tan(30°-A)tan(60°-A)

=1-tan(30°-A)tan(60°-A)+tan(30°-A)tan(60°-A)

=1.

反思 在三角恒等变形中,要注意公式的逆用和变用.

4.化“齐次”法

例4 已知,求下列各式的值.

(1)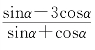;(2)sin2α+sinαcosα+2;(3)

点拨 运用同角三角比的基本关系式,将式子中的sinα,cosα转化为tanα,然后代入求值.

解答 由已知可得tanα=.(www.daowen.com)

反思 形如asinα+bcosα或asin2α+bsinα·cosα+ccos2α的式子分别称为关于sinα,cosα的一次齐次式和二次齐次式,通常涉及弦化切、整体代入、活用“1”的代换等方法.

5.消元法

例5 已知关于x的一元二次方程x2-(tanα+cotα)x+1=0的一个实根是2+3,求sinαcosα的值.

点拨 韦达定理.

解答 将代入,得

又因为.

反思 熟练使用同角三角比的关系.

易错解读

例6 已知sinA=2sinB,tanA=3tanB,则cosA的值为________.

当A在第一、四象限时,;当A在第二、三象限时,

易错分析 上述解法从求解的过程看,似乎没有什么问题,每一步推理都有依据.但仔细分析可以发现这个解法是错误的,错误的原因在于：在三角等式的变形中,改变了A,B的取值范围.由sinA=2sinB变形为cscB=2cscA,A,B的取值由变为A≠kπ,B≠kπ(k∈Z),而当A=kπ,B=kπ时,已知条件中的两个等式都满足,此时,cosA=±1.所以,上述解法产生了漏解现象.

由sinB=0和sinA=2sinB得sinA=0,cosA=±1.

由得,①

当A在第一、四象限时;

当A在第二、三象限时,

当A的终边在x轴上时,cosA=±1.

例7 已知sinθ和cosθ是方程的两个根,求实数θ和m的值.

经典训练

1.若,则θ是(　).

A.第一象限角　B.第二象限角　C.第三象限角　D.第四象限角

2.已知的值.

3.若=_________.

4.若,则sin2x+3sinxcosx-1=_________.

5.设α是第三象限角,问是否存在这样的实数m,使得sinα和cosα是关于x的方程8x2+6mx+2m+1=0的两根？若存在,请求出实数m;若不存在,说明理由.

6.已知,求sinnα+cosnα关于a的表达式.