我们规定：,secα=

2.单位圆：以原点为圆心,以1为半径的圆叫作单位圆.

把点P(x,y)看作角α的终边与单位圆的交点,如图(a)所示.过点P作x轴的垂线,垂足为M.

如图(b)所示,过点A(1,0)作单位圆的切线,设它与角的终边(当α为第一、四象限角时)或其反向延长线(当α为第二、三象限角时)相交于点T.

有向线段MP、OM、AT分别叫作角α的正弦线、余弦线、正切线.

方法简述

1.定义法

例1 已知角θ的顶点为坐标原点,始边为x轴的正半轴,若P(4,y)是角θ终边上一点,且求y的值.

点拨 三角比定义.

反思 通过三角比符号可以初步判断点所在象限.

2.分类讨论思想

例2 已知角θ终边上一点且求cosθ,tanθ.

点拨 根据任意角三角比的定义,知

由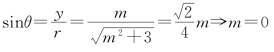或

当时,所以.

反思 解方程时,m=0不能丢,对不同的值分别求相应的三角比.

3.数形结合法

例3 已知集合,求：

(1)A,B;(2)A∩B.

例3答图

解答 由单位圆中的正弦线和余弦线知：

(1)A=;

B=.

(2)A∩B=.

反思 将三角比用单位圆中的有向线段来表示,可以直观地由图求出三角比的取值范围.

易错解读

例4 如果,则α的终边在(　).

A.第三象限

B.第四象限

C.第三或第四象限

D.可能既不在第三象限也不在第四象限(www.daowen.com)

易错分析 本题出错在于学生对象限角概念的不清.象限角的定义是什么?若角的终边落在坐标轴上呢?

例5 已知点P(5t,12t)(t＜0)在角α的终边上,则sinα=__________.

解答 已知点P(5t,12t)(t＜0)在角α的终边上,则

易错分析 本题中所涉及的三角比的定义,含有参数的处理是否进行讨论,是本题的易错点,所以要强化概念内涵.

本题是对三角比定义的考查.可以进一步变式：

(1)若改变点P(5t,12t)(t＜0)在角α的终边上的位置,三角比值是否会改变?

(2)若把条件改为点P(5t,12t)(t≠0)会怎样?为什么三角比会有两个值?此时能否求出角α值?

两个问题看似仅仅改变了字母t的取值,实际上是研究同一终边上不同点位置是否会改变三角比值,是极容易出错之处,不同终边上的点的三角比值是否会改变.同时也考查三角比值确定了,角值是不是确定.

经典训练

1.若sinθ与tanθ异号,则θ是(　).

A.第二象限角　B.第三象限角　C.第一、四象限角　D.第二、三象限角

2.设P(3,y)是角α终边上的一点,若,那么y的值是(　).

A.4　B.±4　C.-4　D.

3.点M(-3t,4t)(t≠0)是角α终边上一点,则有(　).

4.已知角α的终边上有一点P,到原点距离为,且,则P的坐标为___________________.

5.满足等式的α的所有可能值的集合是___________________.

6.已知-π＜α＜π,且,则角α的值是__________________________.

7.若α是第三象限角,且,求角所在的象限.

8.已知角α的终边上有一点P(3a,4a)(a＜0),求sinαtanα的值.

9.若A为△ABC的一个内角,下列三角比哪些可能取负值,哪些不可取负值？

10.求函数f（x）=lg（sinx-cosx）+lg（-sinx-cosx）的定义域.