本节研究了角度制与弧度制的定义,即把弧长等于半径的弧所对的圆心角叫作1弧度角,用符号rad表示.

弧度制与角度制的换算：

1°=弧度≈0.017弧度;1弧度=.

弧长公式和扇形面积公式：

本节解题思想、方法、规律与技巧阐述如下.

方法简述

1.语言转化

由于用弧度制表示的角我们一开始还不大熟悉,不妨将用弧度制表示的角化为用角度制表示角,这样有利于形成解决问题的初步思路.

例1 α和β的和是1弧度,差为1°,则α和β的弧度数分别为________.

点拨 根据规定,用弧度制表示角时,弧度单位一般省略不写.但用角度表示角时,度的记号绝对不能省略,如sin60°不能写成sin60.

解答 由题意可知,α+β=1,α-β=1°=.解方程,可得

反思 弧度与角度的相互关系.

2.形式统一

在对角的度量采用弧度制之后,角的集合与实数集合就建立了对应关系,因此我们可以把角度制中的问题统一到实数集中去解决,这样在角度制所难办到的问题就迎刃而解了.

例2 弓形ABC所在圆的半径为1.如果弓形的弧的长为x,弓形的面积为y,试写出y关于x的函数关系式.

点拨 扇形面积公式应用.

∠AOB=x(弧度),故△OAB的面积为,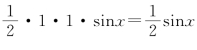

所以.

反思 注意变量的实际范围.

易错解读

例3 已知地球半径为6400千米,地面上一段弧所对的球心角为1',求该弧的弧长.

解答 地球周长=6400×2π=12800π(千米),1'所对弧长=12800π÷360÷60=592.6π(米).

易错分析 角度与弧度的标识不分,混为一谈.

例4 已知,则α-3β的范围是________.(www.daowen.com)

解答 因为α-3β=-α+β（　）+2α-β（　）,又因为,所以

易错分析 此题切不可求出α,β,即这样会使结果的范围扩大,切记.

经典训练

1.把下列各角化成度或弧度,5°=_________弧度;22°30'=_________弧度;125°=________弧度;=_________;=_________;1.5≈_________.

2.2003°是第_________象限角.

3.若角α终边与角β终边关于x轴对称,则α与β的关系是_______________.

4.设角α的终边与的终边关于y轴对称,且α∈(-2π,2π),则α=_____________.

5.已知扇形弧长为30厘米,半径为20厘米,则扇形面积为________.

6.设M={第一象限角},则M∩N是(　).

A.{第一象限角}　B.{锐角}　C.　D.以上都不对

7.2小时30分钟,时钟的分针、时针转过的角分别是(　).

A.π,　B.-π,　C.5π,　D.-5π

8.若α是第三象限的角,则π-α是(　).

A.第一象限的角　B.第二象限的角

C.第三象限的角　D.第四象限的角

9.在直径为10厘米的滑轮上有一条弦,其长为6厘米,且P为弦的中点,滑轮以每秒5弧度的角速度旋转,则经过5秒后,P点转过的弧长是多少？

10.已知α=1690°,

(1)把α写成2kπ+β,k∈Z,β∈(0,2π)的形式;

(2)求θ,使θ与α终边重合,且θ∈(-4π,-2π).

11.若扇形的圆心角是120°,求扇形面积与其内切圆面积的比值.

12.已知扇形OAB的圆心角为150°,面积为平方厘米,求弧AB的长,并求含于扇形内,且以AB为弦的弓形面积.

13.一绳索绕在半径为40厘米的轮圈上,绳索的下端B处悬挂着物体W.如果轮子按逆时针方向每分钟匀速旋转6圈,那么需要几秒才能把物体W的位置向上提升100厘米？(精确到秒)