平面内一条射线绕其端点从初始位置(始边)旋转到终止位置(终边)所形成的图形叫作角.正角：按逆时针方向旋转而形成的角;负角：按顺时针方向旋转而形成的角;零角：一条射线没有作任何旋转而形成的角.象限角：把角的顶点置于坐标原点,角的始边与x轴的正半轴重合,角的终边在第几象限,就说这个角是第几象限角(或者说这个角属于第几象限).与角α的终边相同的角(包括角α本身)的集合为：{β|β=k·360°+α,k∈Z}

方法简述

1.定义法

数学中的定理、性质、公式、法则都是由定义和公理推演而得到的,直接运用定义分析与解决问题便是最直接、最基本、最有效的方法之一,也是研究数学问题的重要途径.

定义法的基本思路是：分析题设条件与求解目标;研究题目中所包含的数学概念与关系;运用数学有关定义将题设条件向解题目标转化.

例1 若α角的终边与-60°的角终边相同,则在-360°到0°内终边与终边相同的角为____.

点拨 突出计算手段,体会用代数在确定角终边的位置中的作用.

解答 α=k·360°-60°,则

反思 终边相同的角不止一个.

2.数形结合思想

在数学问题的解决过程中,将抽象的数学语言与直观的图形结合起来,使“数”的问题,借助“形”去观察,而“形”的问题,借助“数”去思考,实现抽象思维和形象思维的有机结合,使抽象概念与具体图形相互关联和转化,数形结合思想是解决数学问题的有效途径.数形结合思想解题的基本思路是：“形”中觅“数”,即将图形信息部分或全部转换成代数信息,削弱清除“形”的推理部分,使要解决的问题转化为数量关系的讨论;“数”上构“形”,即依据数的结构特征,构造出与之相适应的几何图形,并直观利用图形的特征和规律,解决数的问题;通过以数示形,以形示数,数形互助来求解.

例2 用阴影表示下列集合：

点拨 “终边相同的角”的“形”的相同,必然蕴含着“数”的相似,隐藏着统一的“数量关系”.

解答 在坐标系中分别作出,135°角的终边,如图所示,再用阴影部分表示.注意实线、虚线的区别,得到答案.

例2答图

反思 注意边界的取舍.

3.图形法

例3 已知α是第二象限角,试判断下列各角所在的象限.

(1)2π-α;　(2)π+α.

点拨 对于问题(1),先作角α,再作关于x轴对称的角,得到-α角所在的象限.

解答 如图所示,(1)2π-α在第三象限;(2)π+α在第四象限.

例3答图

反思 也可以直接分析得出正确答案.

4.特殊值法

适当选取符合题目条件的某些特殊值,通过运算、推理或验证,能确定问题的正确答案或否定错误结论,实现简化思维过程、降低推算难度、探索解题思路、寻求解题途径、完善解题过程的目的.特殊值法是探索一般性问题的解题途径的重要方法之一,在特殊情况下的解答过程中,常常蕴含着一般性问题的解题途径和思路.

例4 判断命题是否成立：设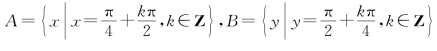,则A是B的真子集.

点拨 关键是找出两个集合的不同元素,可以通分后找相互关系,或者找特例,如元素

集合A中没有.

2k+1必为奇数,k+2则奇偶皆有可能,故可以得出A是B的真子集,此命题为真命题.

反思 通过特殊值进行直观分析推导.

5.枚举法

枚举法也称列举法,就是把题目中的条件(元素)或关系,经过归纳、整理后一一列举出来进行分析、研究的方法.该方法的优点是,它可将较抽象、较复杂的问题具体化、直观化、简单化,从而使数学问题得以顺利解决.例如,集合表示法中的列举法就是将集合中的元素一一列举出来,从而使元素的个数,元素的特征都可一目了然,这样就方便了求解与运算.

例5 写出与下列各角终边相同的角的集合,并把范围在[-360°,720°]内的角写出来.

(1)45°;　(2)-72°.(www.daowen.com)

点拨 通过通解求出特解即可.

解答 (1)α=k·360°+45°,k∈Z.,当k取-1,0,1时的角为-315°,45°,405°;(2)α=k·360°-72°,k∈Z,当k取0,1,2时的角为-72°,288°,648°.

反思 注意终边相同的角的表示方法.

易错解读

例6 判断命题的正确性：终边在第一象限的角是锐角.

解答 锐角的终边落在第一象限,但终边在第一象限的角不一定是锐角,比如390°,所以该命题是假命题.

易错分析 角的概念推广以后,范围变大了,而且有负角了,不可局限于初中的周角范围以内,切不可混淆小于90°的角和锐角等概念.

例7 “θ是第一象限角”是“是第一象限角”的_________条件(填“充分非必要”“必要非充分”“充要”或“既非充分又非必要”).

解答 因为;;

所以横线上填“既非充分又非必要”.

易错分析 注意象限角的概念和终边在坐标轴上的角的区分;以及象限角经过运算后的变化.

经典训练

1.在与1034°角终边相同的角中,最小的正角是_________,最大的负角是_________.

2.若集合M={x|x=k·90°+135°,k∈Z},N={x|x=k·45°+90°,k∈Z},则(　).

A.M=N　B.M⊇N

C.M⊆N　D.M∩N=∅

3.所有与角α终边相同的角可表示为360°·k+α(k∈Z),其中α(　).

A.一定是小于90°的角　B.一定是第一象限的角

C.一定是正角　D.可以是任意角

4.A是与角2007°26'的终边相同的角的集合,则A中适合不等式-360°≤β＜720°的元素β是________________________________.

5.时钟的分针经过2小时40分钟所转过的角是_________,这个角是第_________象限角.

6.与950°的角终边相同的角的集合为_________________________,它是第________象限角,其中最小的正角是___________,最大的负角是_______________.

7.写出终边与下列各处重合的角的集合.

(1)x轴正向;　(2)x轴负向;　(3)y轴正向;　(4)y轴负向;

(5)x轴;　(6)y轴;　(7)坐标轴.

8.已知0°＜β＜360°,且角β的7倍角的终边与角β的终边重合,求角β.

(1)是否存在B=[a,b],使成立？如果存在,求出a,b的范围;如果不存在,说明理由.

(2)是否存在B=[a,b],使A∩B有且仅有4个元素？如果存在,求出b-a的最大范围;如果不存在,说明理由.